Triqonometriya üçbucağın tərəfləri və bucaqları arasındakı əlaqəni öyrənən riyaziyyat sahəsidir. Triqonometrik funksiyalar üçbucağın bucağını onun tərəflərinin uzunluğu ilə əlaqələndirir. Düzbucaqlı üçbucağa münasibətdə altı triqonometrik funksiya var.
p perpendikulyar, h hipotenuza və b ∆ABC düz bucağının əsasıdır. ∆ ABC B nöqtəsində düz bucaq, θ isə p tərəfinə əks olan bucaqdır.
Altı triqonometrik funksiyalar sinus
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendikulyar ∕ Hipotenuz
\(\cos\theta = \) \(\frac{b}{h}\) = Əsas ∕ Hipotenuz
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendikulyar ∕ Əsas
Buna görə \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Beləliklə, üçbucağın çatışmayan bucaqlarını və tərəflərini tapmaq üçün triqonometriyadan istifadə edə bilərik. Aşağıdakı məsələni həll etmək üçün triqonometrik funksiya tətbiq edək.
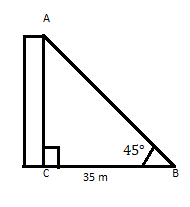
AC üfüqi müstəvidə ayağından 35 m məsafədə üstü 45° bucaq yaradan binadır. Binanın hündürlüyünü tapın.
Biz bilirik ki, \(\tan\theta =\) Perpendikulyar
Kalkulyatordan istifadə edin və sadəcə olaraq bucağın dəyərini dərəcələrlə daxil edin və "sin", "cos" və ya "tan" düyməsini sıxın. Və ya \(\tan 45°\) dəyərini tapmaq üçün aşağıdakı Triqonometrik nisbətlər cədvəlindən istifadə edə bilərsiniz .
| Triqonometrik Funksiya | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| çarpayı | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| san | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Triqonometrik nisbətlər cədvəli 0°, 30°, 45°, 60° və 90° kimi triqonometrik standart bucaqların qiymətlərini tapmağa kömək edir. Triqonometrik nisbətlərdən ibarətdir - sinus, kosinus, tangens, kosekant, sekant, kotangens. Bu nisbətləri sin, cos, tan, cosec, sec və cot kimi qısaca yazmaq olar. Standart bucaqların triqonometrik nisbətlərinin qiymətləri triqonometriya məsələlərini həll etmək üçün vacibdir. Buna görə də bu standart bucaqların triqonometrik nisbətlərinin qiymətlərini yadda saxlamaq lazımdır. Problemlə davam edirik:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Cavab: Binanın hündürlüyü 35 m-dir.
radiusu 1-dir. Dairənin mərkəzi başlanğıc nöqtəsində yerləşir. Beləliklə, mərkəzdən dairənin istənilən nöqtəsinə qədər olan uzunluq 1-dir.
Oxun dairə ilə kəsişdiyi dörd nöqtənin koordinatları (1,0), (0,1), (0,-1), (-1,0) dir. Müsbət bir bucaq yaratmaq üçün saat yönünün əksinə, mənfi bir bucaq üçün isə saat yönünün əksinə hərəkət edirik. θ bucağını x oxundan saat əqrəbinin əksi istiqamətində hərəkət etdirdikdən sonra çevrə üzərində koordinatları (a,b) olan nöqtəni nəzərdən keçirək. P koordinatları (a,b) olan dairənin nöqtəsidir. OPQ üçbucağı Q nöqtəsində düz bucaqlı üçbucaqdır, yəni ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
P nöqtəsindəki koordinatları (cosθ, sinθ) kimi təqdim edə bilərik . Beləliklə, θ-nin kosinusu, bucağın son tərəfinin vahid dairə ilə kəsişdiyi x koordinatlarına, θ-nin sinusu isə bucağın son tərəfinin vahid dairə ilə kəsişdiyi y koordinatlarına bərabərdir. Aşağıdakı vahid dairənin A nöqtəsində y koordinatının qiymətini tapmağa çalışaq.
Cavab: A nöqtəsində Y koordinatı \(\sin 270°\) -dir.
Vahid çevrəsi sinus və kosinus dairəsini bütün real ədədlərə genişləndirməyə imkan verir. İstənilən θ bucağının sin/kosinusunu təyin etmək prosesi aşağıdakı kimidir: