ত্রিকোণমিতি গণিতের একটি শাখা যা একটি ত্রিভুজের বাহু এবং কোণের মধ্যে সম্পর্ক অধ্যয়ন করে। ত্রিকোণমিতিক ফাংশনগুলি একটি ত্রিভুজের কোণকে তার বাহুর দৈর্ঘ্যের সাথে সম্পর্কিত করে। সমকোণ ত্রিভুজের সাথে সম্পর্কিত ছয়টি ত্রিকোণমিতিক ফাংশন রয়েছে।
p হল লম্ব, h হল কর্ণ এবং b হল সমকোণ ∆ABC এর ভিত্তি। ∆ ABC হল B বিন্দুতে একটি সমকোণ এবং θ হল p পাশের বিপরীত কোণ।
ছয়টি ত্রিকোণমিতিক ফাংশন হল সাইন
\(\sin\theta =\) \(\frac{p}{h}\) = লম্ব ∕ হাইপোটেনাস
\(\cos\theta = \) \(\frac{b}{h}\) = ভিত্তি ∕ হাইপোটেনাস
\(\tan\theta =\) \( \frac{p}{b}\) = লম্ব ∕ ভিত্তি
অতএব \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
সুতরাং, আমরা একটি ত্রিভুজের অনুপস্থিত কোণ এবং বাহুগুলি খুঁজে পেতে ত্রিকোণমিতি ব্যবহার করতে পারি। নিচের সমস্যাটি সমাধানের জন্য একটি ত্রিকোণমিতিক ফাংশন প্রয়োগ করা যাক।
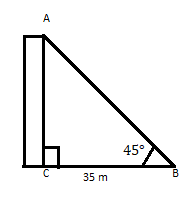
AC একটি বিল্ডিং যার শীর্ষ একটি অনুভূমিক সমতলে তার পা থেকে 35 মিটার দূরত্বে 45° কোণ তৈরি করে। বিল্ডিংয়ের উচ্চতা খুঁজুন।
আমরা জানি যে \(\tan\theta =\) লম্ব
একটি ক্যালকুলেটর ব্যবহার করুন এবং কেবলমাত্র ডিগ্রীতে কোণের মান লিখুন এবং "sin," "cos," বা "tan" বোতামটি চাপুন। অথবা আপনি \(\tan 45°\) এর মান খুঁজে পেতে নীচের ত্রিকোণমিতিক অনুপাত টেবিলটি ব্যবহার করতে পারেন ।
| ত্রিকোণমিতিক ফাংশন | 0° | 30° | 45° | 60° | 90° |
| পাপ | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| কারণ | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| ট্যান | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| খাট | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| সেকেন্ড | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
ত্রিকোণমিতিক অনুপাত সারণী ত্রিকোণমিতিক মানক কোণের মান খুঁজে পেতে সাহায্য করে যেমন 0°, 30°, 45°, 60° এবং 90°। এটি ত্রিকোণমিতিক অনুপাত নিয়ে গঠিত - সাইন, কোসাইন, স্পর্শক, কোসেক্যান্ট, সেকেন্ট, কোট্যাঞ্জেন্ট। এই অনুপাতগুলি সংক্ষেপে sin, cos, tan, cosec, sec এবং cot হিসাবে লেখা যেতে পারে। ত্রিকোণমিতি সমস্যা সমাধানের জন্য আদর্শ কোণের ত্রিকোণমিতিক অনুপাতের মান অপরিহার্য। অতএব, এই মানক কোণগুলির ত্রিকোণমিতিক অনুপাতের মানগুলি মনে রাখা প্রয়োজন। সমস্যাটি চালিয়ে যাওয়া:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
উত্তর: ভবনের উচ্চতা 35 মিটার।
একটি একক বৃত্তের ব্যাসার্ধ 1। বৃত্তের কেন্দ্র উৎপত্তিস্থলে স্থাপন করা হয়। সুতরাং কেন্দ্র থেকে বৃত্তের যেকোনো বিন্দু পর্যন্ত দৈর্ঘ্য 1।
চারটি বিন্দুতে স্থানাঙ্ক যেখানে অক্ষ বৃত্তের সাথে মিলিত হয় তা হল (1,0), (0,1), (0,-1), (-1,0)। একটি ধনাত্মক কোণ করার জন্য আমরা ঘড়ির কাঁটার বিপরীত দিকে এবং একটি ঋণাত্মক কোণের জন্য, আমরা ঘড়ির কাঁটার দিকে সরে যাই। আসুন x-অক্ষ থেকে ঘড়ির কাঁটার বিপরীত দিকে কোণ θ সরানোর পরে একটি বৃত্তে স্থানাঙ্ক (a,b) সহ একটি বিন্দু বিবেচনা করি। P হল স্থানাঙ্ক (a, b) সহ বৃত্তের একটি বিন্দু। ত্রিভুজ OPQ হল Q বিন্দুতে একটি সমকোণ ত্রিভুজ, অর্থাৎ ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
আমরা P বিন্দুতে স্থানাঙ্কগুলিকে (cosθ, sinθ) হিসাবে উপস্থাপন করতে পারি । সুতরাং θ-এর কোসাইন x স্থানাঙ্কের সমান যেখানে কোণের টার্মিনাল দিক একক বৃত্তকে ছেদ করে এবং θ-এর সাইন y স্থানাঙ্কের সমান যেখানে কোণের টার্মিনাল দিক একক বৃত্তকে ছেদ করে। আসুন নীচের একক বৃত্তে A বিন্দুতে y স্থানাঙ্কের মান খুঁজে বের করার চেষ্টা করি।
উত্তর: A বিন্দুতে Y স্থানাঙ্ক হল \(\sin 270°\) ।
একক বৃত্ত আমাদের সাইন এবং কোসাইনের ডোমেইনকে সমস্ত বাস্তব সংখ্যায় প্রসারিত করতে দেয়। যে কোন কোণ θ এর সাইন/কোসাইন নির্ণয় করার প্রক্রিয়াটি নিম্নরূপ: