Trigonometrie ist ein Zweig der Mathematik, der die Beziehung zwischen den Seiten und Winkeln eines Dreiecks untersucht. Trigonometrische Funktionen beziehen den Winkel eines Dreiecks auf die Länge seiner Seiten. Es gibt sechs trigonometrische Funktionen in Bezug auf das rechtwinklige Dreieck.
p ist senkrecht, h ist die Hypotenuse und b ist die Basis des rechten Winkels ∆ABC. ∆ ABC ist ein rechter Winkel am Punkt B und θ ist der Winkel gegenüber der Seite p.
Die sechs trigonometrischen Funktionen sind Sinus
\(\sin\theta =\) \(\frac{p}{h}\) = Senkrecht ∕ Hypotenuse
\(\cos\theta = \) \(\frac{b}{h}\) = Basis ∕ Hypotenuse
\(\tan\theta =\) \( \frac{p}{b}\) = Senkrecht ∕ Basis
Daher \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Daher können wir die Trigonometrie verwenden, um die fehlenden Winkel und Seiten eines Dreiecks zu finden. Wenden wir eine trigonometrische Funktion an, um das folgende Problem zu lösen.
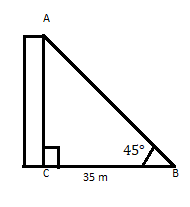
AC ist ein Gebäude, dessen Spitze in einem Abstand von 35 m von seinem Fuß auf einer horizontalen Ebene einen Winkel von 45° bildet. Finden Sie die Höhe des Gebäudes.
Wir wissen, dass \(\tan\theta =\) Senkrecht ist
Verwenden Sie einen Taschenrechner, geben Sie einfach den Winkelwert in Grad ein und drücken Sie die Taste „sin“, „cos“ oder „tan“. Oder Sie können die folgende Tabelle mit trigonometrischen Verhältnissen verwenden, um den Wert von \(\tan 45°\) zu ermitteln .
| Trigonometrische Funktion | 0° | 30° | 45° | 60° | 90° |
| Sünde | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| bräunen | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| Kinderbett | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| Sek | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Die Tabelle der trigonometrischen Verhältnisse hilft dabei, die Werte trigonometrischer Standardwinkel wie 0°, 30°, 45°, 60° und 90° zu ermitteln. Es besteht aus trigonometrischen Verhältnissen – Sinus, Cosinus, Tangens, Kosekans, Sekante, Kotangens. Diese Verhältnisse können kurz als sin, cos, tan, cosec, sec und cot geschrieben werden. Die Werte trigonometrischer Verhältnisse von Standardwinkeln sind für die Lösung trigonometrischer Probleme von wesentlicher Bedeutung. Daher ist es notwendig, sich die Werte der trigonometrischen Verhältnisse dieser Standardwinkel zu merken. Weiter mit dem Problem:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Antwort: Die Höhe des Gebäudes beträgt 35 m.
Ein Einheitskreis hat einen Radius von 1. Der Mittelpunkt des Kreises wird im Ursprung platziert. Die Länge vom Mittelpunkt zu jedem Punkt auf dem Kreis beträgt also 1.
Die Koordinaten an vier Punkten, an denen die Achse den Kreis trifft, sind (1,0), (0,1), (0,-1), (-1,0) . Um einen positiven Winkel zu erzeugen, bewegen wir uns gegen den Uhrzeigersinn und für einen negativen Winkel bewegen wir uns im Uhrzeigersinn. Betrachten wir einen Punkt mit den Koordinaten (a,b) auf einem Kreis, nachdem wir den Winkel θ von der x-Achse aus entgegen dem Uhrzeigersinn verschoben haben. P ist ein Punkt auf dem Kreis mit den Koordinaten (a,b). Das Dreieck OPQ ist ein rechtwinkliges Dreieck im Punkt Q, dh ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Wir können die Koordinaten am Punkt P als (cosθ, sinθ) darstellen . Der Kosinus von θ ist also gleich den x-Koordinaten, wo die Endseite des Winkels den Einheitskreis schneidet, und der Sinus von θ ist gleich den y-Koordinaten, wo die Endseite des Winkels den Einheitskreis schneidet. Versuchen wir, den Wert der y-Koordinate am Punkt A im folgenden Einheitskreis zu ermitteln.
Antwort: Die Y-Koordinate am Punkt A ist \(\sin 270°\) .
Der Einheitskreis ermöglicht es uns, den Bereich von Sinus und Cosinus auf alle reellen Zahlen zu erweitern. Der Prozess zur Bestimmung des Sinus/Cosinus eines beliebigen Winkels θ ist wie folgt: