Trigonometry is a branch of mathematics that studies the relationship between the sides and angles of a triangle. Trigonometric functions relate the angle of a triangle to the length of its sides. There are six trigonometric functions in relation to the right angle triangle.
p is perpendicular, h is the hypotenuse and b is the base of the right-angle ∆ABC. ∆ ABC is a right angle at point B and θ is the angle opposite to side p.
The six trigonometric functions are Sine
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendicular ∕ Hypotenuse
\(\cos\theta = \) \(\frac{b}{h}\)= Base ∕ Hypotenuse
\(\tan\theta =\) \( \frac{p}{b}\)= Perpendicular ∕ Base
Therefore \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\)\( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\)\(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \)\(\frac{b}{p}\)
Hence, we can use trigonometry to find the missing angles and sides of a triangle. Let’s apply a trigonometric function to solve the problem below.
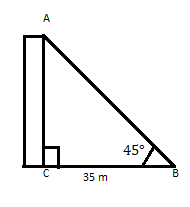
AC is a building whose top makes an angle of 45° at a distance of 35 m from its foot on a horizontal plane. Find the height of the building.
We know that \(\tan\theta =\) Perpendicular
Use a calculator and simply enter the value of the angle in degrees and push the "sin," "cos," or "tan" button. Or you can use the below Trigonometric ratios table to find the value of \(\tan 45°\).
| Trigonometric Function | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| cot | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| sec | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Trigonometric ratios table helps to find the values of trigonometric standard angles such as 0°, 30°, 45°, 60° and 90°. It consists of trigonometric ratios – sine, cosine, tangent, cosecant, secant, cotangent. These ratios can be written in short as sin, cos, tan, cosec, sec and cot. The values of trigonometric ratios of standard angles are essential to solve trigonometry problems. Therefore, it is necessary to remember the values of the trigonometric ratios of these standard angles. Continuing with the problem:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Answer: The height of the building is 35 m.
A unit circle has a radius of 1. The center of the circle is placed at the origin. So the length from the center to any point on the circle is 1.
The coordinates at four points where the axis meet the circle are (1,0), (0,1), (0,-1), (-1,0) . To make a positive angle we move in a counterclockwise direction and for a negative angle, we move in a clockwise direction. Let us consider a point with coordinates (a,b) on a circle after moving angle θ in a counterclockwise direction from x-axis. P is a point on the circle with coordinates (a,b). Triangle OPQ is a right angle triangle at point Q, i.e. ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
We can represent the coordinates at point P as (cosθ, sinθ). So cosine of θ is equal to x coordinates where the terminal side of the angle intersects the unit circle and the sine of θ is equal to y coordinates where the terminal side of the angle intersects the unit circle. Let's try to find the value of the y coordinate at point A in the below unit circle.
Answer: The Y coordinate at point A is \(\sin 270°\).
The unit circle allows us to extend the domain of sine and cosine to all real numbers. The process for determining the sine/cosine of any angle θ is as follows: