La trigonometría es una rama de las matemáticas que estudia la relación entre los lados y los ángulos de un triángulo. Las funciones trigonométricas relacionan el ángulo de un triángulo con la longitud de sus lados. Hay seis funciones trigonométricas en relación con el triángulo rectángulo.
p es perpendicular, h es la hipotenusa y b es la base del ángulo recto ∆ABC. ∆ ABC es un ángulo recto en el punto B y θ es el ángulo opuesto al lado p.
Las seis funciones trigonométricas son Seno
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendicular ∕ Hipotenusa
\(\cos\theta = \) \(\frac{b}{h}\) = Base ∕ Hipotenusa
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendicular ∕ Base
Por lo tanto \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Por lo tanto, podemos usar la trigonometría para encontrar los ángulos y lados faltantes de un triángulo. Apliquemos una función trigonométrica para resolver el siguiente problema.
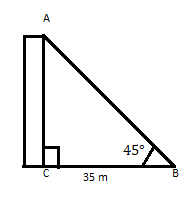
AC es un edificio cuya parte superior forma un ángulo de 45° a una distancia de 35 m de su pie en un plano horizontal. Encuentra la altura del edificio.
Sabemos que \(\tan\theta =\) Perpendicular
Use una calculadora y simplemente ingrese el valor del ángulo en grados y presione el botón "sin", "cos" o "tan". O puede usar la siguiente tabla de razones trigonométricas para encontrar el valor de \(\tan 45°\) .
| Funcion trigonometrica | 0° | 30° | 45° | 60° | 90° |
| pecado | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| porque | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| broncearse | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| cuna | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| segundo | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
La tabla de razones trigonométricas ayuda a encontrar los valores de los ángulos estándar trigonométricos, como 0°, 30°, 45°, 60° y 90°. Consiste en razones trigonométricas: seno, coseno, tangente, cosecante, secante, cotangente. Estas razones se pueden escribir en forma abreviada como sin, cos, tan, cosec, sec y cot. Los valores de las razones trigonométricas de los ángulos estándar son esenciales para resolver problemas de trigonometría. Por lo tanto, es necesario recordar los valores de las razones trigonométricas de estos ángulos estándar. Continuando con el problema:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Respuesta: La altura del edificio es de 35 m.
Un círculo unitario tiene un radio de 1. El centro del círculo se coloca en el origen. Entonces, la longitud desde el centro hasta cualquier punto del círculo es 1.
Las coordenadas en cuatro puntos donde el eje se encuentra con el círculo son (1,0), (0,1), (0,-1), (-1,0) . Para formar un ángulo positivo, nos movemos en sentido contrario a las agujas del reloj y para un ángulo negativo, nos movemos en el sentido de las agujas del reloj. Consideremos un punto con coordenadas (a,b) en un círculo después de mover el ángulo θ en sentido antihorario desde el eje x. P es un punto en el círculo con coordenadas (a,b). El triángulo OPQ es un triángulo rectángulo en el punto Q, es decir, ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Podemos representar las coordenadas en el punto P como (cosθ, sinθ) . Entonces, el coseno de θ es igual a las coordenadas x donde el lado terminal del ángulo interseca al círculo unitario y el seno de θ es igual a las coordenadas y donde el lado terminal del ángulo interseca al círculo unitario. Tratemos de encontrar el valor de la coordenada y en el punto A en el siguiente círculo unitario.
Respuesta: La coordenada Y en el punto A es \(\sin 270°\) .
El círculo unitario nos permite extender el dominio del seno y el coseno a todos los números reales. El proceso para determinar el seno/coseno de cualquier ángulo θ es el siguiente: