مثلثات شاخه ای از ریاضیات است که رابطه بین اضلاع و زوایای مثلث را مطالعه می کند. توابع مثلثاتی زاویه یک مثلث را به طول اضلاع آن مرتبط می کنند. شش تابع مثلثاتی در رابطه با مثلث زاویه قائم وجود دارد.
p عمود است، h فرضیه و b قاعده قائم الزاویه ∆ABC است. ∆ ABC یک زاویه قائمه در نقطه B و θ زاویه مقابل ضلع p است.
شش تابع مثلثاتی عبارتند از: Sine
\(\sin\theta =\) \(\frac{p}{h}\) = عمود بر ∕ Hypotenuse
\(\cos\theta = \) \(\frac{b}{h}\) = پایه ∕ Hypotenuse
\(\tan\theta =\) \( \frac{p}{b}\) = قاعده ∕ عمود بر
بنابراین \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
از این رو، می توانیم از مثلثات برای یافتن زوایای و اضلاع از دست رفته مثلث استفاده کنیم. بیایید یک تابع مثلثاتی برای حل مشکل زیر اعمال کنیم.
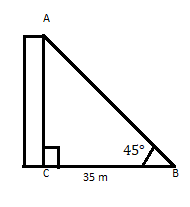
AC ساختمانی است که بالای آن در یک صفحه افقی در فاصله 35 متری از پای خود زاویه 45 درجه ایجاد می کند. ارتفاع ساختمان را پیدا کنید.
می دانیم که \(\tan\theta =\) عمود بر
از یک ماشین حساب استفاده کنید و به سادگی مقدار زاویه را بر حسب درجه وارد کنید و دکمه "sin"، "cos" یا "tan" را فشار دهید. یا می توانید از جدول نسبت های مثلثاتی زیر برای یافتن مقدار \(\tan 45°\) استفاده کنید .
| تابع مثلثاتی | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| تختخواب | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| ثانیه | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
جدول نسبت های مثلثاتی به یافتن مقادیر زوایای استاندارد مثلثاتی مانند 0 درجه، 30 درجه، 45 درجه، 60 درجه و 90 درجه کمک می کند. از نسبتهای مثلثاتی تشکیل شده است - سینوسی، کسینوس، مماس، همزمان، سکونت، کوتانژانت. این نسبت ها را می توان به طور خلاصه به صورت sin، cos، tan، cosec، sec و cot نوشت. مقادیر نسبت های مثلثاتی زوایای استاندارد برای حل مسائل مثلثاتی ضروری است. بنابراین لازم است مقادیر نسبت های مثلثاتی این زوایای استاندارد را به خاطر بسپارید. با مشکل ادامه دهید:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
پاسخ: ارتفاع ساختمان 35 متر است.
یک دایره واحد دارای شعاع 1 است. مرکز دایره در مبدا قرار می گیرد. بنابراین طول از مرکز تا هر نقطه از دایره 1 است.
مختصات چهار نقطه ای که محور به دایره می رسد عبارتند از (1,0), (0,1), (0,-1), (-1,0). برای ایجاد زاویه مثبت در خلاف جهت عقربه های ساعت و برای زاویه منفی در جهت عقربه های ساعت حرکت می کنیم. اجازه دهید پس از حرکت زاویه θ در خلاف جهت عقربه های ساعت از محور x، نقطه ای با مختصات (a,b) روی یک دایره در نظر بگیریم. P نقطه ای از دایره با مختصات (a,b) است. مثلث OPQ یک مثلث قائم الزاویه در نقطه Q است، یعنی ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
می توانیم مختصات نقطه P را به صورت (cosθ، sinθ) نشان دهیم . بنابراین کسینوس θ برابر است با مختصات x در جایی که ضلع انتهایی زاویه دایره واحد را قطع می کند و سینوس θ برابر با مختصات y در جایی است که ضلع انتهایی زاویه دایره واحد را قطع می کند. بیایید سعی کنیم مقدار مختصات y را در نقطه A در دایره واحد زیر پیدا کنیم.
پاسخ: مختصات Y در نقطه A \(\sin 270°\) است.
دایره واحد به ما امکان می دهد دامنه سینوس و کسینوس را به همه اعداد حقیقی گسترش دهیم. فرآیند تعیین سینوس/کسینوس هر زاویه θ به شرح زیر است: