La trigonométrie est une branche des mathématiques qui étudie la relation entre les côtés et les angles d'un triangle. Les fonctions trigonométriques relient l'angle d'un triangle à la longueur de ses côtés. Il existe six fonctions trigonométriques par rapport au triangle rectangle.
p est perpendiculaire, h est l'hypoténuse et b est la base de l'angle droit ∆ABC. ∆ ABC est un angle droit au point B et θ est l'angle opposé au côté p.
Les six fonctions trigonométriques sont Sinus
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendiculaire ∕ Hypoténuse
\(\cos\theta = \) \(\frac{b}{h}\) = Base ∕ Hypoténuse
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendiculaire ∕ Base
Donc \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Par conséquent, nous pouvons utiliser la trigonométrie pour trouver les angles et les côtés manquants d'un triangle. Appliquons une fonction trigonométrique pour résoudre le problème ci-dessous.
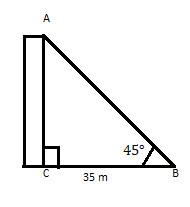
AC est un bâtiment dont le sommet fait un angle de 45° à une distance de 35 m de son pied sur un plan horizontal. Trouver la hauteur du bâtiment.
On sait que \(\tan\theta =\) Perpendiculaire
Utilisez une calculatrice et entrez simplement la valeur de l'angle en degrés et appuyez sur le bouton "sin", "cos" ou "tan". Ou vous pouvez utiliser le tableau des rapports trigonométriques ci-dessous pour trouver la valeur de \(\tan 45°\) .
| Fonction trigonométrique | 0° | 30° | 45° | 60° | 90° |
| péché | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| parce que | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| bronzer | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| lit bébé | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| seconde | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Le tableau des rapports trigonométriques aide à trouver les valeurs des angles trigonométriques standard tels que 0°, 30°, 45°, 60° et 90°. Il se compose de rapports trigonométriques - sinus, cosinus, tangente, cosécante, sécante, cotangente. Ces rapports peuvent être écrits en bref comme sin, cos, tan, cosec, sec et cot. Les valeurs des rapports trigonométriques des angles standards sont essentielles pour résoudre les problèmes de trigonométrie. Par conséquent, il est nécessaire de se souvenir des valeurs des rapports trigonométriques de ces angles standards. Suite du problème :
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Réponse : La hauteur du bâtiment est de 35 m.
Un cercle unité a un rayon de 1. Le centre du cercle est placé à l'origine. Donc la longueur du centre à n'importe quel point du cercle est 1.
Les coordonnées en quatre points où l'axe rencontre le cercle sont (1,0), (0,1), (0,-1), (-1,0) . Pour faire un angle positif, nous nous déplaçons dans le sens inverse des aiguilles d'une montre et pour un angle négatif, nous nous déplaçons dans le sens des aiguilles d'une montre. Considérons un point de coordonnées (a,b) sur un cercle après avoir déplacé l'angle θ dans le sens inverse des aiguilles d'une montre à partir de l'axe des x. P est un point du cercle de coordonnées (a,b). Le triangle OPQ est un triangle rectangle au point Q, soit ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Nous pouvons représenter les coordonnées au point P comme (cosθ, sinθ) . Ainsi, le cosinus de θ est égal aux coordonnées x où le côté terminal de l'angle coupe le cercle unitaire et le sinus de θ est égal aux coordonnées y où le côté terminal de l'angle coupe le cercle unitaire. Essayons de trouver la valeur de la coordonnée y au point A dans le cercle unité ci-dessous.
Réponse : La coordonnée Y au point A est \(\sin 270°\) .
Le cercle unitaire nous permet d'étendre le domaine du sinus et du cosinus à tous les nombres réels. Le processus de détermination du sinus/cosinus de tout angle θ est le suivant :