त्रिकोणमिति गणित की एक शाखा है जो त्रिभुज की भुजाओं और कोणों के बीच संबंध का अध्ययन करती है। त्रिकोणमितीय फलन त्रिभुज के कोण को उसकी भुजाओं की लंबाई से संबंधित करते हैं। समकोण त्रिभुज के संबंध में छह त्रिकोणमितीय कार्य हैं।
p लंब है, h कर्ण है और b समकोण ∆ABC का आधार है। ∆ ABC बिंदु B पर एक समकोण है और θ भुजा p के विपरीत कोण है।
छह त्रिकोणमितीय कार्य साइन हैं
\(\sin\theta =\) \(\frac{p}{h}\) = लंब ∕ कर्ण
\(\cos\theta = \) \(\frac{b}{h}\) = आधार ∕ कर्ण
\(\tan\theta =\) \( \frac{p}{b}\) = लंब ∕ आधार
इसलिए \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
इसलिए, हम त्रिकोणमिति का उपयोग किसी त्रिभुज के लापता कोणों और भुजाओं को खोजने के लिए कर सकते हैं। आइए नीचे दी गई समस्या को हल करने के लिए एक त्रिकोणमितीय फ़ंक्शन लागू करें।
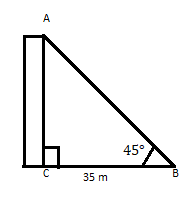
एसी एक इमारत है जिसका शीर्ष क्षैतिज तल पर अपने पैर से 35 मीटर की दूरी पर 45 डिग्री का कोण बनाता है। भवन की ऊँचाई ज्ञात कीजिए।
हम जानते हैं कि \(\tan\theta =\) लंबवत
एक कैलकुलेटर का उपयोग करें और बस कोण के मान को डिग्री में दर्ज करें और "sin," "cos," या "tan" बटन दबाएं। या \(\tan 45°\) का मान ज्ञात करने के लिए आप निम्न त्रिकोणमितीय अनुपात तालिका का उपयोग कर सकते हैं ।
| त्रिकोणमितीय समारोह | 0 डिग्री | 30° | 45° | 60 डिग्री | 90° |
| पाप | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| ओल | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| टैन | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| खाट | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| सेकंड | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
त्रिकोणमितीय अनुपात तालिका त्रिकोणमितीय मानक कोणों जैसे 0°, 30°, 45°, 60° और 90° के मानों को खोजने में मदद करती है। इसमें त्रिकोणमितीय अनुपात होते हैं - साइन, कोसाइन, स्पर्शरेखा, कोसेकेंट, सेकेंट, कॉटैंजेंट। इन अनुपातों को संक्षेप में sin, cos, tan, cosec, sec और cot के रूप में लिखा जा सकता है। त्रिकोणमिति समस्याओं को हल करने के लिए मानक कोणों के त्रिकोणमितीय अनुपातों के मान आवश्यक हैं। इसलिए, इन मानक कोणों के त्रिकोणमितीय अनुपातों के मूल्यों को याद रखना आवश्यक है। समस्या जारी है:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
उत्तर: भवन की ऊँचाई 35 मीटर है।
एक इकाई वृत्त की त्रिज्या 1 होती है। वृत्त के केंद्र को मूल बिंदु पर रखा जाता है। अतः केंद्र से वृत्त के किसी बिंदु तक की लंबाई 1 है।
चार बिंदुओं पर निर्देशांक (1,0), (0,1), (0,-1), (-1,0) हैं। धनात्मक कोण बनाने के लिए हम वामावर्त दिशा में चलते हैं और ऋणात्मक कोण के लिए हम दक्षिणावर्त दिशा में चलते हैं। आइए x-अक्ष से वामावर्त दिशा में कोण θ को घुमाने के बाद एक वृत्त पर निर्देशांक (a,b) के साथ एक बिंदु पर विचार करें। P वृत्त पर एक बिंदु है जिसके निर्देशांक (a,b) हैं। त्रिभुज OPQ बिन्दु Q पर एक समकोण त्रिभुज है, अर्थात् ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
हम बिंदु P पर निर्देशांकों को (cosθ, sinθ) के रूप में निरूपित कर सकते हैं । तो θ का कोज्या x निर्देशांक के बराबर है जहां कोण का टर्मिनल पक्ष यूनिट सर्कल को काटता है और θ की साइन y निर्देशांक के बराबर है जहां कोण का टर्मिनल पक्ष यूनिट सर्कल को काटता है। आइए नीचे दिए गए यूनिट सर्कल में बिंदु A पर y निर्देशांक का मान ज्ञात करने का प्रयास करें।
उत्तर: बिंदु A पर Y निर्देशांक \(\sin 270°\) है।
यूनिट सर्कल हमें साइन और कोसाइन के डोमेन को सभी वास्तविक संख्याओं तक विस्तारित करने की अनुमति देता है। किसी भी कोण θ की ज्या/कोज्या निर्धारित करने की प्रक्रिया इस प्रकार है: