Trigonometrija je grana matematike koja proučava odnos između stranica i kutova trokuta. Trigonometrijske funkcije povezuju kut trokuta s duljinom njegovih stranica. Postoji šest trigonometrijskih funkcija u odnosu na pravokutni trokut.
p je okomica, h je hipotenuza i b je osnovica pravokutnog ∆ABC. ∆ ABC je pravi kut u točki B, a θ je kut nasuprot stranici p.
Šest trigonometrijskih funkcija su sinus
\(\sin\theta =\) \(\frac{p}{h}\) = okomica ∕ hipotenuza
\(\cos\theta = \) \(\frac{b}{h}\) = baza ∕ hipotenuza
\(\tan\theta =\) \( \frac{p}{b}\) = okomica ∕ baza
Stoga \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Dakle, možemo koristiti trigonometriju za pronalaženje kutova i stranica trokuta koji nedostaju. Primijenimo trigonometrijsku funkciju da riješimo problem u nastavku.
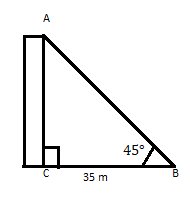
AC je građevina čiji vrh na udaljenosti 35 m od podnožja na horizontalnoj ravnini zaklapa kut od 45°. Pronađite visinu zgrade.
Znamo da je \(\tan\theta =\) okomito
Koristite kalkulator i jednostavno unesite vrijednost kuta u stupnjevima i pritisnite gumb "sin", "cos" ili "tan". Ili možete koristiti donju tablicu trigonometrijskih omjera da pronađete vrijednost \(\tan 45°\) .
| Trigonometrijska funkcija | 0° | 30° | 45° | 60° | 90° |
| grijeh | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| preplanuli ten | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| dječji krevetić | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| sek | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Tablica trigonometrijskih omjera pomaže pronaći vrijednosti standardnih trigonometrijskih kutova kao što su 0°, 30°, 45°, 60° i 90°. Sastoji se od trigonometrijskih omjera - sinusa, kosinusa, tangensa, kosakana, sekansa, kotangensa. Ovi se omjeri mogu ukratko napisati kao sin, cos, tan, cosec, sec i cot. Vrijednosti trigonometrijskih omjera standardnih kutova bitne su za rješavanje trigonometrijskih problema. Stoga je potrebno zapamtiti vrijednosti trigonometrijskih omjera ovih standardnih kutova. Nastavljamo s problemom:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Odgovor: Visina objekta je 35 m.
Jedinična kružnica ima polumjer 1. Središte kružnice nalazi se u ishodištu. Dakle, duljina od središta do bilo koje točke kruga je 1.
Koordinate u četiri točke gdje se os susreće s krugom su (1,0), (0,1), (0,-1), (-1,0) . Za pozitivan kut pomičemo se u smjeru suprotnom od kazaljke na satu, a za negativni kut pomičemo se u smjeru kazaljke na satu. Promotrimo točku s koordinatama (a,b) na kružnici nakon pomicanja kuta θ u smjeru suprotnom od kazaljke na satu od x-osi. P je točka na kružnici s koordinatama (a,b). Trokut OPQ je pravokutni trokut u točki Q, tj. ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Koordinate u točki P možemo prikazati kao (cosθ, sinθ) . Dakle, kosinus od θ jednak je x koordinatama gdje krajnja stranica kuta siječe jediničnu kružnicu, a sinus od θ jednak je y koordinatama gdje krajnja stranica kuta siječe jediničnu kružnicu. Pokušajmo pronaći vrijednost y koordinate u točki A u donjem jediničnom krugu.
Odgovor: Y koordinata u točki A je \(\sin 270°\) .
Jedinična kružnica nam omogućuje da proširimo domenu sinusa i kosinusa na sve realne brojeve. Postupak određivanja sinusa/kosinusa bilo kojeg kuta θ je sljedeći: