Trigonometri adalah cabang matematika yang mempelajari hubungan antara sisi dan sudut segitiga. Fungsi trigonometri menghubungkan sudut segitiga dengan panjang sisi-sisinya. Ada enam fungsi trigonometri dalam kaitannya dengan segitiga siku-siku.
p tegak lurus, h adalah sisi miring dan b adalah alas sudut siku-siku ∆ABC. ∆ ABC adalah sudut siku-siku di titik B dan θ adalah sudut yang berhadapan dengan sisi p.
Keenam fungsi trigonometri adalah Sinus
\(\sin\theta =\) \(\frac{p}{h}\) = Tegak Lurus ∕ Sisi Miring
\(\cos\theta = \) \(\frac{b}{h}\) = Basis ∕ Sisi Miring
\(\tan\theta =\) \( \frac{p}{b}\) = Tegak Lurus ∕ Alas
Oleh karena itu \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Oleh karena itu, kita dapat menggunakan trigonometri untuk menemukan sudut dan sisi segitiga yang hilang. Mari terapkan fungsi trigonometri untuk menyelesaikan soal di bawah ini.
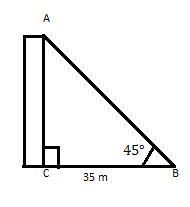
AC adalah bangunan yang bagian atasnya membentuk sudut 45° pada jarak 35 m dari kakinya pada bidang mendatar. Temukan ketinggian bangunan.
Kita tahu bahwa \(\tan\theta =\) Tegak Lurus
Gunakan kalkulator dan cukup masukkan nilai sudut dalam derajat dan tekan tombol "sin", "cos", atau "tan". Atau Anda dapat menggunakan tabel rasio trigonometri di bawah ini untuk mencari nilai \(\tan 45°\) .
| Fungsi trigonometri | 0° | 30° | 45° | 60° | 90° |
| dosa | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| cokelat | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| pondok | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| detik | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Tabel rasio trigonometri membantu menemukan nilai sudut standar trigonometri seperti 0°, 30°, 45°, 60° dan 90°. Ini terdiri dari rasio trigonometri - sinus, cosinus, tangen, cosecan, secan, cotangen. Perbandingan ini dapat dituliskan sebagai sin, cos, tan, cosec, sec dan cot. Nilai perbandingan trigonometri sudut standar sangat penting untuk menyelesaikan soal trigonometri. Oleh karena itu, perlu diingat nilai perbandingan trigonometri dari sudut standar tersebut. Melanjutkan masalah:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Jawab: Tinggi gedung adalah 35 m.
Sebuah lingkaran satuan memiliki jari-jari 1. Pusat lingkaran ditempatkan pada titik asal. Jadi panjang dari titik pusat ke sembarang titik pada lingkaran adalah 1.
Koordinat di empat titik pertemuan sumbu lingkaran adalah (1,0), (0,1), (0,-1), (-1,0) . Untuk membuat sudut positif kita bergerak berlawanan arah jarum jam dan untuk sudut negatif kita bergerak searah jarum jam. Mari kita perhatikan titik dengan koordinat (a,b) pada lingkaran setelah memindahkan sudut θ berlawanan arah jarum jam dari sumbu x. P adalah titik pada lingkaran dengan koordinat (a,b). Segitiga OPQ adalah segitiga siku-siku di titik Q, yaitu ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Kita dapat menyatakan koordinat pada titik P sebagai (cosθ, sinθ) . Jadi cosinus θ sama dengan koordinat x di mana sisi terminal sudut memotong lingkaran satuan dan sinus θ sama dengan koordinat y di mana sisi terminal sudut memotong lingkaran satuan. Mari kita coba mencari nilai koordinat y di titik A pada lingkaran satuan di bawah ini.
Jawab: Koordinat Y di titik A adalah \(\sin 270°\) .
Lingkaran satuan memungkinkan kita memperluas domain sinus dan cosinus ke semua bilangan real. Proses untuk menentukan sinus/kosinus dari sembarang sudut θ adalah sebagai berikut: