La trigonometria è una branca della matematica che studia la relazione tra i lati e gli angoli di un triangolo. Le funzioni trigonometriche mettono in relazione l'angolo di un triangolo con la lunghezza dei suoi lati. Ci sono sei funzioni trigonometriche in relazione al triangolo ad angolo retto.
p è perpendicolare, h è l'ipotenusa e b è la base dell'angolo retto ∆ABC. ∆ ABC è un angolo retto nel punto B e θ è l'angolo opposto al lato p.
Le sei funzioni trigonometriche sono Seno
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendicolare ∕ Ipotenusa
\(\cos\theta = \) \(\frac{b}{h}\) = Base ∕ Ipotenusa
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendicolare ∕ Base
Pertanto \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Quindi, possiamo usare la trigonometria per trovare gli angoli e i lati mancanti di un triangolo. Applichiamo una funzione trigonometrica per risolvere il problema sottostante.
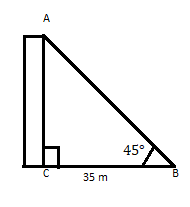
AC è un edificio la cui sommità forma un angolo di 45° ad una distanza di 35 m dal suo piede su un piano orizzontale. Trova l'altezza dell'edificio.
Sappiamo che \(\tan\theta =\) Perpendicolare
Usa una calcolatrice e inserisci semplicemente il valore dell'angolo in gradi e premi il pulsante "sin", "cos" o "tan". Oppure puoi utilizzare la tabella dei rapporti trigonometrici sottostante per trovare il valore di \(\tan 45°\) .
| Funzione trigonometrica | 0° | 30° | 45° | 60° | 90° |
| peccato | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| abbronzatura | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| culla | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| sec | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
La tabella dei rapporti trigonometrici aiuta a trovare i valori degli angoli standard trigonometrici come 0°, 30°, 45°, 60° e 90°. Consiste di rapporti trigonometrici: seno, coseno, tangente, cosecante, secante, cotangente. Questi rapporti possono essere scritti in breve come sin, cos, tan, cosec, sec e cot. I valori dei rapporti trigonometrici degli angoli standard sono essenziali per risolvere problemi di trigonometria. Pertanto, è necessario ricordare i valori dei rapporti trigonometrici di questi angoli standard. Proseguendo con il problema:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Risposta: L'altezza dell'edificio è di 35 m.
Una circonferenza unitaria ha raggio 1. Il centro della circonferenza è posto nell'origine. Quindi la lunghezza dal centro a qualsiasi punto della circonferenza è 1.
Le coordinate nei quattro punti in cui l'asse incontra il cerchio sono (1,0), (0,1), (0,-1), (-1,0) . Per creare un angolo positivo ci muoviamo in senso antiorario e per un angolo negativo ci muoviamo in senso orario. Consideriamo un punto con coordinate (a,b) su un cerchio dopo aver spostato l'angolo θ in senso antiorario dall'asse x. P è un punto sulla circonferenza di coordinate (a,b). Il triangolo OPQ è un triangolo ad angolo retto nel punto Q, cioè ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Possiamo rappresentare le coordinate nel punto P come (cosθ, sinθ) . Quindi il coseno di θ è uguale alle coordinate x dove il lato terminale dell'angolo interseca la circonferenza unitaria e il seno di θ è uguale alle coordinate y dove il lato terminale dell'angolo interseca la circonferenza unitaria. Proviamo a trovare il valore della coordinata y nel punto A nella circonferenza unitaria sottostante.
Risposta: La coordinata Y nel punto A è \(\sin 270°\) .
La circonferenza unitaria ci permette di estendere il dominio di seno e coseno a tutti i numeri reali. Il processo per determinare il seno/coseno di qualsiasi angolo θ è il seguente: