三角法は、三角形の辺と角度の関係を研究する数学の分野です。三角関数は、三角形の角度と辺の長さを関連付けます。直角三角形に関しては 6 つの三角関数があります。
pは垂直、 hは斜辺、 bは直角 ΔABC の底辺です。 ΔABCは点Bにおける直角、θは辺pの反対側の角度です。
6 つの三角関数は、サイン
\(\sin\theta =\) \(\frac{p}{h}\) = 垂線 ∕ 斜辺
\(\cos\theta = \) \(\frac{b}{h}\) = 底辺 ∕ 斜辺
\(\tan\theta =\) \( \frac{p}{b}\) = 垂線 ∕ 底辺
したがって\( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
したがって、三角法を使用して、三角形の不足している角度と辺を見つけることができます。三角関数を適用して以下の問題を解いてみましょう。
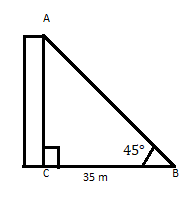
ACは、水平面上で足元から35mの距離で頂部が45°の角度をなす建物です。建物の高さを求めます。
\(\tan\theta =\)垂直
電卓を使用して角度の値を度単位で入力し、「sin」、「cos」、または「tan」ボタンを押すだけです。または、以下の三角比の表を使用して\(\tan 45°\)の値を見つけることもできます。
| 三角関数 | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| タン | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| コット | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| コ秒 | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| 秒 | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
三角比表は、0°、30°、45°、60°、90°などの三角法の標準角度の値を見つけるのに役立ちます。これは、三角比 (サイン、コサイン、タンジェント、コセカント、セカント、コタンジェント) で構成されます。これらの比率は、sin、cos、tan、cosec、sec、cot と短く書くことができます。標準角度の三角比の値は、三角法の問題を解くために不可欠です。したがって、これらの標準角度の三角比の値を覚えておく必要があります。問題を続けます:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
答え: 建物の高さは 35 メートルです。
単位円の半径は 1 です。円の中心は原点に配置されます。したがって、円周上の中心から点までの長さは 1 になります。
軸と円が交わる 4 つの点の座標は (1,0)、(0,1)、(0,-1)、(-1,0) です。正の角度を作るには反時計回りに移動し、負の角度を作るには時計回りに移動します。 x軸から反時計回りに角度θだけ移動させた円上の座標(a,b)の点を考えます。 P は、座標 (a,b) を持つ円上の点です。三角形 OPQ は点 Q における直角三角形、つまり ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
点 P の座標は (cosθ, sinθ) として表すことができます。したがって、θ の余弦は、角度の終端側が単位円と交差する x 座標に等しく、θ の正弦は、角度の終端側が単位円と交差する y 座標に等しくなります。以下の単位円内の点 A の y 座標の値を求めてみましょう。
答え:点 A の Y 座標は\(\sin 270°\)です。
単位円を使用すると、サインとコサインの領域をすべての実数に拡張できます。任意の角度 θ のサイン/コサインを決定するプロセスは次のとおりです。