Тригонометријата е гранка на математиката која го проучува односот помеѓу страните и аглите на триаголникот. Тригонометриските функции го поврзуваат аголот на триаголникот со должината на неговите страни. Постојат шест тригонометриски функции во однос на триаголникот од прав агол.
p е нормално, h е хипотенузата и b е основата на правоаголниот ∆ABC. ∆ ABC е прав агол во точката B и θ е аголот спротивен на страната p.
Шесте тригонометриски функции се синус
\(\sin\theta =\) \(\frac{p}{h}\) = Перпендикуларна ∕ Хипотенуза
\(\cos\theta = \) \(\frac{b}{h}\) = База ∕ Хипотенуза
\(\tan\theta =\) \( \frac{p}{b}\) = Нормална ∕ основа
Затоа \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Оттука, можеме да ја користиме тригонометријата за да ги најдеме аглите и страните што недостасуваат на триаголникот. Ајде да примениме тригонометриска функција за да го решиме проблемот подолу.
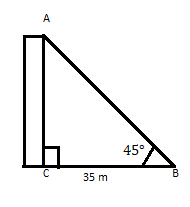
AC е зграда чиј врв прави агол од 45° на растојание од 35 m од неговото подножје на хоризонтална рамнина. Најдете ја висината на зградата.
Знаеме дека \(\tan\theta =\) Нормално
Користете калкулатор и едноставно внесете ја вредноста на аголот во степени и притиснете го копчето „sin“, „cos“ или „tan“. Или можете да ја користите долунаведената табела со тригонометриски соодноси за да ја пронајдете вредноста на \(\tan 45°\) .
| Тригонометриска функција | 0° | 30° | 45° | 60° | 90° |
| грев | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| креветче | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| сек | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Табелата со тригонометриски соодноси помага да се пронајдат вредностите на тригонометриските стандардни агли како што се 0°, 30°, 45°, 60° и 90°. Се состои од тригонометриски соодноси - синус, косинус, тангента, косеканта, секанта, котангента. Овие соодноси можат да се напишат накратко како sin, cos, tan, cosec, sec и cot. Вредностите на тригонометриските соодноси на стандардните агли се од суштинско значење за решавање на тригонометриските проблеми. Затоа, неопходно е да се запаметат вредностите на тригонометриските соодноси на овие стандардни агли. Продолжувајќи со проблемот:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Одговор: Висината на зградата е 35 m.
Единечниот круг има радиус 1. Центарот на кругот е поставен на почетокот. Значи, должината од центарот до која било точка на кругот е 1.
Координатите на четири точки каде што оската се среќава со кругот се (1,0), (0,1), (0,-1), (-1,0) . За да направиме позитивен агол се движиме спротивно од стрелките на часовникот, а за негативен агол се движиме во насока на стрелките на часовникот. Да разгледаме точка со координати (a,b) на круг откако ќе се движи аголот θ во спротивна насока од стрелките на часовникот од оската x. P е точка на кружницата со координати (a,b). Триаголникот OPQ е правоаголен триаголник во точката Q, т.е. ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Можеме да ги претставиме координатите во точката P како (cosθ, sinθ) . Значи, косинус на θ е еднаков на x координати каде што крајната страна на аголот ја сече единечната кружница, а синусот на θ е еднаков на y координатите каде што крајната страна на аголот ја сече единечната круг. Ајде да се обидеме да ја најдеме вредноста на y координатата во точката А во долунаведената единична кружница.
Одговор: Y координатата во точката A е \(\sin 270°\) .
Кругот на единицата ни овозможува да го прошириме доменот на синус и косинус на сите реални броеви. Процесот за одредување на синус/косинус на кој било агол θ е како што следува: