Тригонометр бол гурвалжны талууд ба өнцгийн хоорондын хамаарлыг судалдаг математикийн салбар юм. Тригонометрийн функцууд нь гурвалжны өнцгийг түүний талуудын урттай харьцуулдаг. Тэгш өнцөгт гурвалжинтай холбоотой зургаан тригонометрийн функц байдаг.
p нь перпендикуляр, h нь гипотенуз, b нь ∆ABC тэгш өнцөгтийн суурь юм. ∆ ABC нь B цэг дээрх тэгш өнцөг, θ нь p талын эсрэг талын өнцөг юм.
Зургаан тригонометрийн функцууд нь Синус
\(\sin\theta =\) \(\frac{p}{h}\) = Перпендикуляр ∕ Гипотенуз
\(\cos\theta = \) \(\frac{b}{h}\) = Үндсэн ∕ Гипотенуз
\(\tan\theta =\) \( \frac{p}{b}\) = Перпендикуляр ∕ Суурь
Тиймээс \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Тиймээс бид гурвалжны алга болсон өнцөг болон талуудыг олохын тулд тригонометрийг ашиглаж болно. Доорх асуудлыг шийдэхийн тулд тригонометрийн функцийг ашиглая.
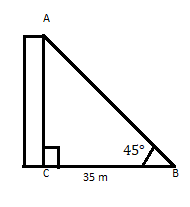
АС гэдэг нь хэвтээ хавтгайд хөлөөсөө 35 м-ийн зайд дээд тал нь 45° өнцөг үүсгэдэг барилга юм. Барилгын өндрийг ол.
\(\tan\theta =\) Перпендикуляр
Тооцоологч ашиглаад өнцгийн утгыг градусаар оруулаад "нүгэл", "кос" эсвэл "тан" товчийг дарна уу. Эсвэл та доорх тригонометрийн харьцааны хүснэгтийг ашиглан \(\tan 45°\) утгыг олох боломжтой .
| Тригонометрийн функц | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| ор | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| косек | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| сек | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Тригонометрийн харьцааны хүснэгт нь 0°, 30°, 45°, 60°, 90° зэрэг тригонометрийн стандарт өнцгийн утгыг олоход тусална. Энэ нь тригонометрийн харьцаанаас бүрдэнэ - синус, косинус, тангенс, косекант, секант, котангенс. Эдгээр харьцааг sin, cos, tan, cosec, sec, cot гэж товчоор бичиж болно. Стандарт өнцгийн тригонометрийн харьцааны утгууд нь тригонометрийн асуудлыг шийдвэрлэхэд зайлшгүй шаардлагатай. Тиймээс эдгээр стандарт өнцгүүдийн тригонометрийн харьцааны утгыг санах хэрэгтэй. Асуудлыг үргэлжлүүлэх:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Хариулт: Барилгын өндөр нь 35 м.
Нэгж тойргийн радиус нь 1. Тойргийн төв нь эх цэг дээр байрладаг. Тэгэхээр төвөөс тойргийн дурын цэг хүртэлх урт нь 1 байна.
Тэнхлэгийг тойрогтой нийлэх дөрвөн цэгийн координатууд нь (1,0), (0,1), (0,-1), (-1,0) байна. Эерэг өнцөг үүсгэхийн тулд бид цагийн зүүний эсрэг, сөрөг өнцгийн хувьд цагийн зүүний дагуу хөдөлдөг. Х тэнхлэгээс цагийн зүүний эсрэг чиглэлд θ өнцгийг хөдөлгөсний дараа тойрог дээрх (a,b) координаттай цэгийг авч үзье. P нь (a,b) координаттай тойрог дээрх цэг юм. OPQ гурвалжин нь Q цэг дээрх тэгш өнцөгт гурвалжин, өөрөөр хэлбэл ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Бид P цэг дээрх координатуудыг (cosθ, sinθ) гэж илэрхийлж болно . Тэгэхээр θ-ийн косинус нь өнцгийн төгсгөл тал нь нэгж тойргийг огтолж байгаа х координаттай, θ-ийн синус нь өнцгийн төгсгөл тал нь нэгж тойрогтой огтлолцох y координаттай тэнцүү байна. Доорх нэгж тойргийн А цэг дээрх у координатын утгыг олохыг оролдъё.
Хариулт: А цэг дээрх Y координат нь \(\sin 270°\) байна.
Нэгж тойрог нь синус ба косинусын мужийг бүх бодит тоонуудад өргөтгөх боломжийг олгодог. Аливаа θ өнцгийн синус/косинусыг тодорхойлох үйл явц нь дараах байдалтай байна: