Trigonometry သည် တြိဂံတစ်ခု၏ ဘေးနှစ်ဖက်နှင့် ထောင့်များကြားရှိ ဆက်နွယ်မှုကို လေ့လာသော သင်္ချာဘာသာရပ်ခွဲတစ်ခုဖြစ်သည်။ Trigonometric လုပ်ဆောင်ချက်များသည် တြိဂံတစ်ခု၏ထောင့်ကို ၎င်း၏နှစ်ဖက်၏အရှည်နှင့် ဆက်စပ်သည်။ ထောင့်မှန်တြိဂံနှင့်ဆက်စပ်၍ trigonometric function ခြောက်ခုရှိသည်။

p သည် ထောင့်မှန်၊ h သည် hypotenuse ဖြစ်ပြီး b သည် ညာဘက်ထောင့် ∆ABC ၏ အခြေခံဖြစ်သည်။ ∆ ABC သည် အမှတ် B တွင် ထောင့်မှန်ဖြစ်ပြီး θ သည် ဘေးဘက် p နှင့် ဆန့်ကျင်ဘက်ထောင့်ဖြစ်သည်။
Trigonometric လုပ်ဆောင်ချက် ခြောက်ခု မှာ Sine (sin) ၊ Cosine ( cos )၊ Tangent (tan ) ၊ Cosecant (csc) ၊ Secant (sec) နှင့် Cotangent( cot) ။ နောက်ဆုံးလုပ်ဆောင်ချက်သုံးခုသည် ပထမလုပ်ဆောင်ချက်သုံးခု၏ အပြန်အလှန်အကျိုးသက်ရောက်မှုဖြစ်သည်။
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendicular ∕ Hypotenuse
\(\cos\theta = \) \(\frac{b}{h}\) = အခြေခံ ∕ Hypotenuse
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendicular ∕ အခြေခံ
ထို့ကြောင့် \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
ထို့ကြောင့်၊ တြိဂံတစ်ခု၏ ပျောက်ဆုံးနေသောထောင့်များနှင့် နှစ်ဖက်ကိုရှာဖွေရန် trigonometry ကိုသုံးနိုင်သည်။ အောက်ပါပြဿနာကိုဖြေရှင်းရန် trigonometric function ကိုသုံးကြပါစို့။
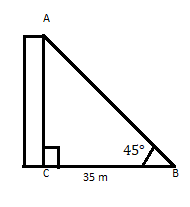
AC သည် အလျားလိုက်လေယာဉ်ပေါ်ရှိ ၎င်း၏ခြေမှ ၃၅ မီတာအကွာအဝေးတွင် ၄၅° ထောင့်ချိုးရှိသော အဆောက်အဦတစ်ခုဖြစ်သည်။ အဆောက်အဦး၏အမြင့်ကိုရှာပါ။
\(\tan\theta =\) Perpendicular (P) ∕ Base (B) ၊ ဤနေရာတွင် \(\tan45=\frac{p}{35}\)
ဂဏန်းပေါင်းစက်ကိုသုံး၍ ထောင့်တန်ဖိုးကို ဒီဂရီဖြင့် ရိုက်ထည့်ကာ "sin" "cos" သို့မဟုတ် "tan" ခလုတ်ကို နှိပ်ပါ။ သို့မဟုတ် \(\tan 45°\) ၏တန်ဖိုးကိုရှာဖွေရန် အောက်ပါ Trigonometric အချိုးများဇယားကို အသုံးပြုနိုင်သည် ။
| Trigonometric Function | ၀ံ | 30° | 45° | 60° | 90° |
| အပြစ် | ၀ယ်တယ်။ | ၁/၂ | \(\sqrt2/2\) | \(\sqrt3/2\) | ၁ |
| cos | ၁ | \(\sqrt3/2\) | \(\sqrt2/2\) | ၁/၂ | ၀ယ်တယ်။ |
| အသားရောင် | ၀ယ်တယ်။ | \(\sqrt3/3\) | ၁ | \(\sqrt3\) | ∞ |
| ကုတင် | ∞ | \(\sqrt3\) | ၁ | \(\frac{1}{\sqrt3}\) | ၀ယ်တယ်။ |
| cosec | ∞ | ၂ | \(\sqrt2 \) | \(2/\sqrt3\) | ၁ |
| စက္ကန့် | ၁ | \(2/\sqrt3\) | \(\sqrt2 \) | ၂ | ∞ |
Trigonometric ratios table သည် 0°၊ 30°၊ 45°၊ 60° နှင့် 90° ကဲ့သို့သော trigonometric standard angles များ၏ တန်ဖိုးများကို ရှာဖွေရန် ကူညီပေးပါသည်။ ၎င်းတွင် trigonometric အချိုးများ- sine၊ cosine၊ tangent၊ cosecant၊ secant၊ cotangent တို့ ပါဝင်သည်။ ဤအချိုးများကို sin, cos, tan, cosec, sec နှင့် cot အဖြစ် အတိုချုံးရေးနိုင်သည်။ စံထောင့်များ၏ trigonometric အချိုးတန်ဖိုးများသည် trigonometry ပြဿနာများကိုဖြေရှင်းရန်အတွက် မရှိမဖြစ်လိုအပ်ပါသည်။ ထို့ကြောင့်၊ ဤစံထောင့်များ၏ trigonometric အချိုးတန်ဖိုးများကို မှတ်သားထားရန် လိုအပ်ပါသည်။ ပြဿနာနှင့် ဆက်နေသည်-
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
အဖြေ - အဆောက်အဦ၏အမြင့်မှာ 35 မီတာဖြစ်သည်။
ယူနစ်စက်ဝိုင်း
ယူနစ်စက်ဝိုင်းတစ်ခုတွင် အချင်းဝက် 1 ရှိသည်။ စက်ဝိုင်း၏ဗဟိုကို မူလနေရာတွင် ထားရှိသည်။ ထို့ကြောင့် စက်ဝိုင်းပေါ်ရှိ မည်သည့်အမှတ်သို့မဆို အလျားသည် 1 ဖြစ်သည်။

ဝင်ရိုးသည် စက်ဝိုင်းနှင့်တွေ့ဆုံသည့် အမှတ်လေးခုရှိ သြဒိနိတ်များမှာ (1,0), (0,1), (0,-1), (-1,0) ဖြစ်သည်။ ကျွန်ုပ်တို့သည် အပြုသဘောဆောင်သောထောင့်ကို နာရီလက်တံပြောင်းပြန်ဦးတည်ချက်ဖြင့် ရွေ့လျားရန်နှင့် အနုတ်ထောင့်အတွက်၊ ကျွန်ုပ်တို့သည် နာရီလက်တံအတိုင်း ဦးတည်ရွေ့လျားသည်။ ထောင့် θ ရွေ့လျားပြီးနောက် စက်ဝိုင်းတွင် သြဒိနိတ်များ (a,b) ပါသော အမှတ်ကို x-axis မှ တန်ပြန်ဦးတည်ချက်ဖြင့် သုံးသပ်ကြည့်ကြစို့။ P သည် သြဒိနိတ်များ (a၊b) ရှိသော စက်ဝိုင်းရှိ အမှတ်တစ်ခုဖြစ်သည်။ တြိဂံ OPQ သည် အမှတ် Q တွင် ထောင့်မှန်တြိဂံဖြစ်သည်၊ ဆိုလိုသည်မှာ ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
ကျွန်ုပ်တို့သည် အမှတ် P တွင် သြဒိနိတ်များကို (cosθ၊ sinθ) အဖြစ် ကိုယ်စားပြုနိုင်သည် ။ ထို့ကြောင့် θ ၏ cosine သည် ထောင့်၏ terminal side သည် ယူနစ်စက်ဝိုင်းကို ဖြတ်သည့်နေရာတွင် x သြဒိနိတ်များနှင့် ညီမျှပြီး θ ၏ sine သည် ထောင့်၏ terminal side သည် ယူနစ်စက်ဝိုင်းကိုဖြတ်သည့် y သြဒိနိတ်များနှင့် ညီမျှသည်။ အောက်ပါယူနစ်စက်ဝိုင်းရှိ အမှတ် A တွင် y သြဒိနိတ်တန်ဖိုးကို ရှာကြည့်ရအောင်။

အဖြေ- အမှတ် A တွင် Y သြဒိနိတ်သည် \(\sin 270°\) ဖြစ်သည်။
ယူနစ်စက်ဝိုင်းသည် ကျွန်ုပ်တို့အား ကိန်းစစ်များအားလုံးသို့ sine နှင့် cosine ၏ဒိုမိန်းကို တိုးချဲ့နိုင်စေပါသည်။ မည်သည့်ထောင့် θ ၏ sine/cosine ကို ဆုံးဖြတ်ရန် လုပ်ငန်းစဉ်မှာ အောက်ပါအတိုင်းဖြစ်သည် ။
- (1,0) မှ စတင်၍ သင့်အနေအထား၊ မူလနှင့် အပြုသဘောဆောင်သော x-ဝင်ရိုးကြားရှိ ထောင့်ကို θ နှင့် ညီမျှသည့်တိုင်အောင် နာရီလက်တံပြောင်းပြန် ဦးတည်ချက်အတိုင်း ယူနစ်စက်ဝိုင်းအတိုင်း ရွေ့ပါ။
- \(\sin θ\) သည် သင့်အမှတ်၏ y-coordinate နှင့် ညီမျှပြီး၊ \(\cos θ\) သည် x-coordinate နှင့် ညီမျှသည်။
