त्रिकोणमिति गणितको एउटा शाखा हो जसले त्रिभुजको पक्ष र कोणहरू बीचको सम्बन्धको अध्ययन गर्छ। त्रिकोणमितीय प्रकार्यहरूले त्रिकोणको कोणलाई यसको पक्षहरूको लम्बाइसँग सम्बन्धित गर्दछ। समकोण त्रिकोणको सम्बन्धमा छवटा त्रिकोणमितीय कार्यहरू छन्।
p लम्ब हुन्छ, h कर्ण हो र b समकोण ∆ABC को आधार हो। ∆ ABC बिन्दु B मा समकोण हो र θ पक्ष p को विपरित कोण हो।
छ त्रिकोणमितीय प्रकार्यहरू साइन हुन्
\(\sin\theta =\) \(\frac{p}{h}\) = लम्बवत ∕ हाइपोटेन्युज
\(\cos\theta = \) \(\frac{b}{h}\) = आधार ∕ हाइपोटेन्युज
\(\tan\theta =\) \( \frac{p}{b}\) = लम्बवत ∕ आधार
त्यसैले \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
तसर्थ, हामी त्रिभुजको छुटेको कोण र भुजाहरू पत्ता लगाउन त्रिकोणमिति प्रयोग गर्न सक्छौं। तलको समस्या समाधान गर्न त्रिकोणमितीय प्रकार्य लागू गरौं।
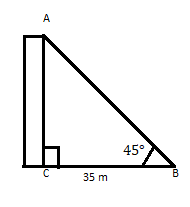
AC एउटा भवन हो जसको शीर्षले तेर्सो समतलमा आफ्नो खुट्टाबाट 35 मिटरको दूरीमा 45° को कोण बनाउँछ। भवनको उचाइ पत्ता लगाउनुहोस्।
हामीलाई थाहा छ कि \(\tan\theta =\) लम्बवत
क्याल्कुलेटर प्रयोग गर्नुहोस् र केवल डिग्रीमा कोणको मान प्रविष्ट गर्नुहोस् र "sin," "cos," वा "tan" बटन थिच्नुहोस्। वा \(\tan 45°\) को मान पत्ता लगाउन तलको त्रिकोणमितीय अनुपात तालिका प्रयोग गर्न सक्नुहुन्छ ।
| त्रिकोणमितीय प्रकार्य | ०° | ३०° | ४५° | ६०° | ९०° |
| पाप | ० | १/२ | \(\sqrt2/2\) | \(\sqrt3/2\) | १ |
| cos | १ | \(\sqrt3/2\) | \(\sqrt2/2\) | १/२ | ० |
| ट्यान | ० | \(\sqrt3/3\) | १ | \(\sqrt3\) | ∞ |
| खाट | ∞ | \(\sqrt3\) | १ | \(\frac{1}{\sqrt3}\) | ० |
| cosec | ∞ | २ | \(\sqrt2 \) | \(2/\sqrt3\) | १ |
| सेकेन्ड | १ | \(2/\sqrt3\) | \(\sqrt2 \) | २ | ∞ |
त्रिकोणमितीय अनुपात तालिकाले 0°, 30°, 45°, 60° र 90° जस्ता त्रिकोणमितीय मानक कोणहरूको मानहरू पत्ता लगाउन मद्दत गर्दछ। यसमा त्रिकोणमितीय अनुपातहरू हुन्छन् - साइन, कोसाइन, ट्यान्जेन्ट, कोसेकन्ट, सेकन्ट, कोट्यान्जेन्ट। यी अनुपातहरूलाई sin, cos, tan, cosec, sec र cot को रूपमा छोटोमा लेख्न सकिन्छ। त्रिकोणमिति समस्याहरू समाधान गर्न मानक कोणहरूको त्रिकोणमितीय अनुपातहरूको मानहरू आवश्यक छन्। त्यसकारण, यी मानक कोणहरूको त्रिकोणमितीय अनुपातहरूको मानहरू सम्झनु आवश्यक छ। समस्या संग जारी:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
उत्तर: भवनको उचाइ ३५ मिटर छ।
एक एकाइ सर्कलको त्रिज्या 1 हुन्छ। सर्कलको केन्द्र उत्पत्तिमा राखिएको छ। त्यसैले केन्द्रबाट वृत्तको कुनै पनि बिन्दुसम्मको लम्बाइ 1 हो।
अक्षले वृत्तसँग मिल्ने चारवटा बिन्दुहरूमा रहेको निर्देशांकहरू (1,0), (0,1), (0,-1), (-1,0) हुन्। सकारात्मक कोण बनाउनको लागि हामी घडीको विपरीत दिशामा जान्छौं र नकारात्मक कोणको लागि, हामी घडीको दिशामा सर्छौं। x-अक्षबाट घडीको विपरीत दिशामा कोण θ घुमाएपछि वृत्तमा निर्देशांक (a,b) भएको बिन्दुलाई विचार गरौं। P निर्देशांक (a, b) भएको वृत्तमा रहेको बिन्दु हो। त्रिभुज OPQ बिन्दु Q मा समकोण त्रिभुज हो, अर्थात ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
हामी बिन्दु P मा निर्देशांकहरूलाई (cosθ, sinθ) को रूपमा प्रतिनिधित्व गर्न सक्छौं । त्यसैले θ को कोसाइन x कोसाइन बराबर हुन्छ जहाँ कोणको टर्मिनल पक्षले एकाइ सर्कललाई छेउछ र θ को साइन y निर्देशांक बराबर हुन्छ जहाँ कोणको टर्मिनल पक्षले एकाइ सर्कललाई छेउछ। तलको एकाइ सर्कलमा बिन्दु A मा y समन्वयको मान पत्ता लगाउने प्रयास गरौं।
उत्तर: बिन्दु A मा Y समन्वय \(\sin 270°\) हो।
एकाइ सर्कलले हामीलाई साइन र कोसाइनको डोमेनलाई सबै वास्तविक संख्याहरूमा विस्तार गर्न अनुमति दिन्छ। कुनै पनि कोण θ को साइन/कोसाइन निर्धारण गर्ने प्रक्रिया निम्नानुसार छ: