Trigonometrie is een tak van de wiskunde die de relatie tussen de zijden en hoeken van een driehoek bestudeert. Trigonometrische functies relateren de hoek van een driehoek aan de lengte van de zijden. Er zijn zes trigonometrische functies met betrekking tot de rechthoekige driehoek.
p is loodrecht, h is de schuine zijde en b is het grondvlak van de rechte hoek ∆ABC. ∆ ABC is een rechte hoek in punt B en θ is de hoek tegenover zijde p.
De zes goniometrische functies zijn sinus
\(\sin\theta =\) \(\frac{p}{h}\) = Loodrecht ∕ Hypotenusa
\(\cos\theta = \) \(\frac{b}{h}\) = Basis ∕ Hypotenusa
\(\tan\theta =\) \( \frac{p}{b}\) = Loodrecht ∕ Basis
Daarom \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Daarom kunnen we trigonometrie gebruiken om de ontbrekende hoeken en zijden van een driehoek te vinden. Laten we een trigonometrische functie toepassen om het onderstaande probleem op te lossen.
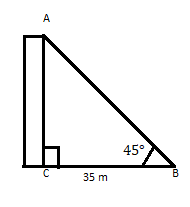
AC is een gebouw waarvan de bovenkant een hoek maakt van 45° op een afstand van 35 m vanaf de voet op een horizontaal vlak. Zoek de hoogte van het gebouw.
We weten dat \(\tan\theta =\) Loodrecht
Gebruik een rekenmachine en voer eenvoudig de waarde van de hoek in graden in en druk op de knop "sin", "cos" of "tan". Of u kunt de onderstaande tabel met goniometrische verhoudingen gebruiken om de waarde van \(\tan 45°\) te vinden .
| Trigonometrische functie | 0° | 30° | 45° | 60° | 90° |
| zonde | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| bruinen | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| kinderbed | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| sec | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Trigonometrische verhoudingentabel helpt bij het vinden van de waarden van trigonometrische standaardhoeken zoals 0°, 30°, 45°, 60° en 90°. Het bestaat uit trigonometrische verhoudingen - sinus, cosinus, tangens, cosecans, secans, cotangens. Deze verhoudingen kunnen kort worden geschreven als sin, cos, tan, cosec, sec en cot. De waarden van trigonometrische verhoudingen van standaardhoeken zijn essentieel om trigonometrische problemen op te lossen. Daarom is het noodzakelijk om de waarden van de trigonometrische verhoudingen van deze standaardhoeken te onthouden. Verder met het probleem:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Antwoord: De hoogte van het gebouw is 35 m.
Een eenheidscirkel heeft een straal van 1. Het middelpunt van de cirkel wordt in de oorsprong geplaatst. Dus de lengte van het middelpunt tot elk punt op de cirkel is 1.
De coördinaten op vier punten waar de as de cirkel raakt zijn (1,0), (0,1), (0,-1), (-1,0) . Om een positieve hoek te maken bewegen we tegen de klok in en voor een negatieve hoek bewegen we met de klok mee. Laten we eens kijken naar een punt met coördinaten (a,b) op een cirkel na verplaatsing van hoek θ tegen de klok in vanaf de x-as. P is een punt op de cirkel met coördinaten (a,b). Driehoek OPQ is een rechthoekige driehoek in punt Q, dwz ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
We kunnen de coördinaten in punt P voorstellen als (cosθ, sinθ) . Dus cosinus van θ is gelijk aan x-coördinaten waar de eindzijde van de hoek de eenheidscirkel snijdt en de sinus van θ is gelijk aan y-coördinaten waar de eindzijde van de hoek de eenheidscirkel snijdt. Laten we proberen de waarde van de y-coördinaat op punt A in de onderstaande eenheidscirkel te vinden.
Antwoord: De Y-coördinaat in punt A is \(\sin 270°\) .
Met de eenheidscirkel kunnen we het domein van sinus en cosinus uitbreiden naar alle reële getallen. Het proces voor het bepalen van de sinus/cosinus van elke hoek θ is als volgt: