Trygonometria jest gałęzią matematyki, która bada związek między bokami i kątami trójkąta. Funkcje trygonometryczne wiążą kąt trójkąta z długością jego boków. Istnieje sześć funkcji trygonometrycznych w odniesieniu do trójkąta prostokątnego.
p jest prostopadła, h jest przeciwprostokątną, a b jest podstawą kąta prostego ∆ABC. ∆ ABC jest kątem prostym w punkcie B, a θ jest kątem przeciwległym do boku p.
Sześć funkcji trygonometrycznych to sinusoidy
\(\sin\theta =\) \(\frac{p}{h}\) = Prostopadła ∕ Przeciwprostokątna
\(\cos\theta = \) \(\frac{b}{h}\) = Podstawa ∕ Przeciwprostokątna
\(\tan\theta =\) \( \frac{p}{b}\) = prostopadła ∕ podstawa
Dlatego \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Dlatego możemy użyć trygonometrii, aby znaleźć brakujące kąty i boki trójkąta. Zastosujmy funkcję trygonometryczną, aby rozwiązać poniższy problem.
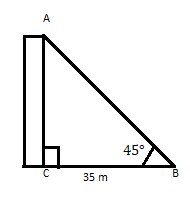
AC to budynek, którego wierzchołek tworzy kąt 45° w odległości 35 m od jego podstawy na płaszczyźnie poziomej. Znajdź wysokość budynku.
Wiemy, że \(\tan\theta =\) prostopadła
Użyj kalkulatora i po prostu wprowadź wartość kąta w stopniach i naciśnij przycisk „sin”, „cos” lub „tan”. Możesz też skorzystać z poniższej tabeli stosunków trygonometrycznych, aby znaleźć wartość \(\tan 45°\) .
| Funkcja trygonometryczna | 0° | 30° | 45° | 60° | 90° |
| grzech | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| sałata | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| dębnik | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| łóżko składane | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosek | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| sek | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Tabela stosunków trygonometrycznych pomaga znaleźć wartości trygonometrycznych kątów standardowych, takich jak 0°, 30°, 45°, 60° i 90°. Składa się ze stosunków trygonometrycznych – sinus, cosinus, tangens, cosecans, secans, cotangens. Współczynniki te można zapisać w skrócie jako sin, cos, tan, cosec, sec i cot. Wartości stosunków trygonometrycznych kątów standardowych są niezbędne do rozwiązywania problemów trygonometrii. Dlatego konieczne jest zapamiętanie wartości stosunków trygonometrycznych tych standardowych kątów. Kontynuując problem:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Odp.: Wysokość budynku wynosi 35 m.
Okrąg jednostkowy ma promień 1. Środek okręgu znajduje się w początku układu współrzędnych. Zatem długość od środka do dowolnego punktu na okręgu wynosi 1.
Współrzędne w czterech punktach, w których osie stykają się z okręgiem, to (1,0), (0,1), (0,-1), (-1,0) . Aby uzyskać kąt dodatni, poruszamy się w kierunku przeciwnym do ruchu wskazówek zegara, a dla kąta ujemnego poruszamy się w kierunku zgodnym z ruchem wskazówek zegara. Rozważmy punkt o współrzędnych (a,b) na okręgu po przesunięciu kąta θ w kierunku przeciwnym do ruchu wskazówek zegara od osi x. P jest punktem na okręgu o współrzędnych (a,b). Trójkąt OPQ jest trójkątem prostokątnym w punkcie Q, czyli ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Możemy przedstawić współrzędne w punkcie P jako (cosθ, sinθ) . Tak więc cosinus θ jest równy współrzędnej x, gdzie końcowa strona kąta przecina okrąg jednostkowy, a sinus θ jest równy współrzędnej y, gdzie końcowa strona kąta przecina okrąg jednostkowy. Spróbujmy znaleźć wartość współrzędnej y w punkcie A na poniższym okręgu jednostkowym.
Odpowiedź: Współrzędna Y w punkcie A to \(\sin 270°\) .
Okrąg jednostkowy pozwala nam rozszerzyć dziedzinę sinusa i cosinusa na wszystkie liczby rzeczywiste. Proces wyznaczania sinusa/cosinusa dowolnego kąta θ jest następujący: