A trigonometria é um ramo da matemática que estuda a relação entre os lados e os ângulos de um triângulo. As funções trigonométricas relacionam o ângulo de um triângulo com o comprimento de seus lados. Existem seis funções trigonométricas em relação ao triângulo retângulo.
p é perpendicular, h é a hipotenusa e b é a base do ângulo reto ∆ABC. ∆ ABC é um ângulo reto no ponto B e θ é o ângulo oposto ao lado p.
As seis funções trigonométricas são Seno
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendicular ∕ Hipotenusa
\(\cos\theta = \) \(\frac{b}{h}\) = Base ∕ Hipotenusa
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendicular ∕ Base
Portanto \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Portanto, podemos usar a trigonometria para encontrar os ângulos e lados ausentes de um triângulo. Vamos aplicar uma função trigonométrica para resolver o problema abaixo.
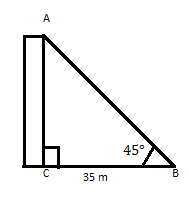
AC é um edifício cujo topo faz um ângulo de 45° a uma distância de 35 m de seu pé em um plano horizontal. Encontre a altura do edifício.
Sabemos que \(\tan\theta =\) Perpendicular
Use uma calculadora e simplesmente insira o valor do ângulo em graus e pressione o botão "sin", "cos" ou "tan". Ou você pode usar a tabela de proporções trigonométricas abaixo para encontrar o valor de \(\tan 45°\) .
| Função trigonométrica | 0° | 30° | 45° | 60° | 90° |
| pecado | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| porque | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| bronzeado | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| berço | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| segundo | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
A tabela de razões trigonométricas ajuda a encontrar os valores dos ângulos padrão trigonométricos, como 0°, 30°, 45°, 60° e 90°. Consiste em razões trigonométricas – seno, cosseno, tangente, cossecante, secante, cotangente. Essas razões podem ser escritas resumidamente como sin, cos, tan, cosec, sec e cot. Os valores das razões trigonométricas dos ângulos padrão são essenciais para resolver problemas de trigonometria. Portanto, é necessário lembrar os valores das razões trigonométricas desses ângulos padrão. Continuando com o problema:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Resposta: A altura do prédio é de 35 m.
Um círculo unitário tem um raio de 1. O centro do círculo é colocado na origem. Portanto, o comprimento do centro a qualquer ponto do círculo é 1.
As coordenadas em quatro pontos onde o eixo encontra o círculo são (1,0), (0,1), (0,-1), (-1,0) . Para fazer um ângulo positivo nos movemos no sentido anti-horário e para um ângulo negativo nos movemos no sentido horário. Consideremos um ponto com coordenadas (a,b) em um círculo depois de mover o ângulo θ no sentido anti-horário a partir do eixo x. P é um ponto no círculo com coordenadas (a,b). O triângulo OPQ é um triângulo retângulo no ponto Q, ou seja, ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Podemos representar as coordenadas no ponto P como (cosθ, sinθ) . Portanto, o cosseno de θ é igual às coordenadas x onde o lado terminal do ângulo intercepta o círculo unitário e o seno de θ é igual às coordenadas y onde o lado terminal do ângulo intercepta o círculo unitário. Vamos tentar encontrar o valor da coordenada y no ponto A no círculo unitário abaixo.
Resposta: A coordenada Y no ponto A é \(\sin 270°\) .
O círculo unitário nos permite estender o domínio do seno e cosseno para todos os números reais. O processo para determinar o seno/cosseno de qualquer ângulo θ é o seguinte: