Тригонометрия — это раздел математики, изучающий отношения между сторонами и углами треугольника. Тригонометрические функции связывают угол треугольника с длиной его сторон. Существует шесть тригонометрических функций по отношению к прямоугольному треугольнику.
p — перпендикуляр, h — гипотенуза, b — основание прямого угла ∆ABC. ∆ ABC — прямой угол в точке B, а θ — угол, противоположный стороне p.
Шесть тригонометрических функций представляют собой синус.
\(\sin\theta =\) \(\frac{p}{h}\) = Перпендикуляр ∕ Гипотенуза
\(\cos\theta = \) \(\frac{b}{h}\) = основание ∕ гипотенуза
\(\tan\theta =\) \( \frac{p}{b}\) = Перпендикуляр ∕ Основание
Поэтому \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Следовательно, мы можем использовать тригонометрию, чтобы найти недостающие углы и стороны треугольника. Применим тригонометрическую функцию для решения приведенной ниже задачи.
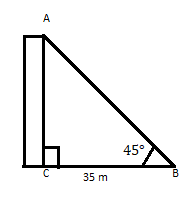
АС — здание, вершина которого образует угол 45° на расстоянии 35 м от его подножия в горизонтальной плоскости. Найдите высоту здания.
Мы знаем, что \(\tan\theta =\) перпендикулярно
Используйте калькулятор и просто введите значение угла в градусах и нажмите кнопку «sin», «cos» или «tan». Или вы можете использовать приведенную ниже таблицу тригонометрических соотношений , чтобы найти значение \(\tan 45°\) .
| Тригонометрическая функция | 0° | 30° | 45° | 60° | 90° |
| грех | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| потому что | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| загар | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| детская кроватка | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| сек | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Таблица тригонометрических соотношений помогает найти значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°. Он состоит из тригонометрических соотношений – синуса, косинуса, тангенса, косеканса, секанса, котангенса. Эти соотношения могут быть записаны кратко как sin, cos, tan, cosec, sec и cot. Значения тригонометрических отношений стандартных углов необходимы для решения задач тригонометрии. Поэтому необходимо запомнить значения тригонометрических отношений этих стандартных углов. Продолжение проблемы:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Ответ: Высота дома 35 м.
Единичный круг имеет радиус 1. Центр круга находится в начале координат. Значит, длина от центра до любой точки окружности равна 1.
Координаты в четырех точках, где ось встречается с окружностью, равны (1,0), (0,1), (0,-1), (-1,0) . Чтобы получить положительный угол, мы движемся против часовой стрелки, а чтобы получить отрицательный угол, мы движемся по часовой стрелке. Рассмотрим точку с координатами (a,b) на окружности после перемещения на угол θ против часовой стрелки от оси x. P — точка на окружности с координатами (a,b). Треугольник OPQ является прямоугольным треугольником в точке Q, т. е. ∠ PQO = 90°.
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Мы можем представить координаты в точке P как (cosθ, sinθ) . Таким образом, косинус θ равен координатам x, где конечная сторона угла пересекает единичную окружность, а синус θ равен координатам y, где конечная сторона угла пересекает единичную окружность. Попробуем найти значение координаты y в точке A на единичном круге ниже.
Ответ: Координата Y в точке A равна \(\sin 270°\) .
Единичный круг позволяет нам расширить область значений синуса и косинуса на все действительные числа. Процесс определения синуса/косинуса любого угла θ выглядит следующим образом: