Trigonometria është një degë e matematikës që studion marrëdhëniet midis brinjëve dhe këndeve të një trekëndëshi. Funksionet trigonometrike lidhin këndin e një trekëndëshi me gjatësinë e brinjëve të tij. Ekzistojnë gjashtë funksione trigonometrike në lidhje me trekëndëshin kënddrejtë.
p është pingul, h është hipotenuza dhe b është baza e këndit të drejtë ∆ABC. ∆ ABC është një kënd i drejtë në pikën B dhe θ është këndi përballë brinjës p.
Gjashtë funksionet trigonometrike janë Sine
\(\sin\theta =\) \(\frac{p}{h}\) = pingul ∕ Hipotenuzë
\(\cos\theta = \) \(\frac{b}{h}\) = Baza ∕ Hipotenuza
\(\tan\theta =\) \( \frac{p}{b}\) = pingul ∕ Baza
Prandaj \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Prandaj, ne mund të përdorim trigonometrinë për të gjetur këndet dhe brinjët që mungojnë të një trekëndëshi. Le të aplikojmë një funksion trigonometrik për të zgjidhur problemin e mëposhtëm.
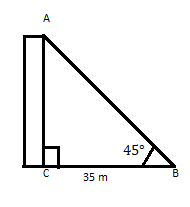
AC është një ndërtesë maja e së cilës bën një kënd prej 45° në një distancë prej 35 m nga këmbët e saj në një plan horizontal. Gjeni lartësinë e ndërtesës.
Ne e dimë se \(\tan\theta =\) pingul
Përdorni një kalkulator dhe thjesht futni vlerën e këndit në gradë dhe shtypni butonin "sin", "cos" ose "tan". Ose mund të përdorni tabelën e raporteve trigonometrike më poshtë për të gjetur vlerën e \(\tan 45°\) .
| Funksioni trigonometrik | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| ahur | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| sek | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Tabela e raporteve trigonometrike ndihmon për të gjetur vlerat e këndeve standarde trigonometrike si 0°, 30°, 45°, 60° dhe 90°. Ai përbëhet nga raportet trigonometrike - sinus, kosinus, tangjentë, kosekant, sekant, kotangjent. Këto raporte mund të shkruhen shkurt si sin, cos, tan, cosec, sec dhe cot. Vlerat e raporteve trigonometrike të këndeve standarde janë thelbësore për zgjidhjen e problemeve të trigonometrisë. Prandaj, është e nevojshme të mbani mend vlerat e raporteve trigonometrike të këtyre këndeve standarde. Duke vazhduar me problemin:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Përgjigje: Lartësia e objektit është 35 m.
Një rreth njësi ka një rreze prej 1. Qendra e rrethit vendoset në origjinë. Pra, gjatësia nga qendra në çdo pikë të rrethit është 1.
Koordinatat në katër pika ku boshti takohet me rrethin janë (1,0), (0,1), (0,-1), (-1,0) . Për të krijuar një kënd pozitiv lëvizim në drejtim të kundërt të akrepave të orës dhe për një kënd negativ lëvizim në drejtim të akrepave të orës. Le të shqyrtojmë një pikë me koordinata (a,b) në një rreth pas lëvizjes së këndit θ në drejtim të kundërt të akrepave të orës nga boshti x. P është një pikë në rrethin me koordinata (a,b). Trekëndëshi OPQ është një trekëndësh kënddrejtë në pikën Q, p.sh. ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Ne mund t'i paraqesim koordinatat në pikën P si (cosθ, sinθ) . Pra, kosinusi i θ është i barabartë me x koordinatat ku ana fundore e këndit kryqëzon rrethin njësi dhe sinusi i θ është i barabartë me koordinatat y ku ana fundore e këndit e pret rrethin njësi. Le të përpiqemi të gjejmë vlerën e koordinatës y në pikën A në rrethin e njësisë më poshtë.
Përgjigje: Koordinata Y në pikën A është \(\sin 270°\) .
Rrethi i njësisë na lejon të zgjerojmë domenin e sinusit dhe kosinusit në të gjithë numrat realë. Procesi për përcaktimin e sinusit/kosinusit të çdo këndi θ është si vijon: