Trigonometri är en gren av matematiken som studerar förhållandet mellan sidorna och vinklarna i en triangel. Trigonometriska funktioner relaterar vinkeln på en triangel till längden på dess sidor. Det finns sex trigonometriska funktioner i förhållande till den rätvinkliga triangeln.
p är vinkelrät, h är hypotenusan och b är basen för den räta vinkeln ∆ABC. ∆ ABC är en rät vinkel i punkt B och θ är vinkeln motsatt sidan p.
De sex trigonometriska funktionerna är sinus
\(\sin\theta =\) \(\frac{p}{h}\) = Vinkelrät ∕ Hypotenus
\(\cos\theta = \) \(\frac{b}{h}\) = Bas ∕ Hypotenus
\(\tan\theta =\) \( \frac{p}{b}\) = Vinkelrät ∕ Bas
Därför \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Därför kan vi använda trigonometri för att hitta de saknade vinklarna och sidorna i en triangel. Låt oss använda en trigonometrisk funktion för att lösa problemet nedan.
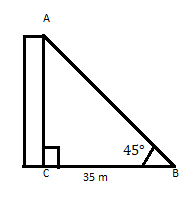
AC är en byggnad vars topp bildar en vinkel på 45° på ett avstånd av 35 m från foten på ett horisontellt plan. Hitta höjden på byggnaden.
Vi vet att \(\tan\theta =\) vinkelrät
Använd en miniräknare och ange helt enkelt värdet på vinkeln i grader och tryck på "sin", "cos" eller "tan"-knappen. Eller så kan du använda tabellen nedan för trigonometriska förhållanden för att hitta värdet på \(\tan 45°\) .
| Trigonometrisk funktion | 0° | 30° | 45° | 60° | 90° |
| synd | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| solbränna | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| spjälsäng | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| sek | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Tabellen med trigonometriska förhållanden hjälper till att hitta värdena för trigonometriska standardvinklar som 0°, 30°, 45°, 60° och 90°. Den består av trigonometriska förhållanden - sinus, cosinus, tangent, cosecant, sekant, cotangens. Dessa förhållanden kan kort skrivas som sin, cos, tan, cosec, sec och cot. Värdena på trigonometriska förhållanden för standardvinklar är viktiga för att lösa trigonometriproblem. Därför är det nödvändigt att komma ihåg värdena för de trigonometriska förhållandena för dessa standardvinklar. Fortsätter med problemet:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Svar: Byggnadens höjd är 35 m.
En enhetscirkel har en radie på 1. Cirkelns centrum placeras vid origo. Så längden från mitten till valfri punkt på cirkeln är 1.
Koordinaterna vid fyra punkter där axeln möter cirkeln är (1,0), (0,1), (0,-1), (-1,0) . För att göra en positiv vinkel rör vi oss moturs och för en negativ vinkel rör vi oss i medurs riktning. Låt oss betrakta en punkt med koordinater (a,b) på en cirkel efter att ha flyttat vinkeln θ i moturs riktning från x-axeln. P är en punkt på cirkeln med koordinater (a,b). Triangel OPQ är en rätvinklig triangel i punkt Q, dvs ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Vi kan representera koordinaterna i punkt P som (cosθ, sinθ) . Så cosinus för θ är lika med x-koordinater där terminalsidan av vinkeln skär enhetscirkeln och sinus för θ är lika med y-koordinater där terminalsidan av vinkeln skär enhetscirkeln. Låt oss försöka hitta värdet på y-koordinaten vid punkt A i enhetscirkeln nedan.
Svar: Y-koordinaten i punkt A är \(\sin 270°\) .
Enhetscirkeln tillåter oss att utöka domänen av sinus och cosinus till alla reella tal. Processen för att bestämma sinus/cosinus för valfri vinkel θ är som följer: