Trigonometry ni tawi la hisabati ambalo husoma uhusiano kati ya pande na pembe za pembetatu. Kazi za trigonometric huhusisha pembe ya pembetatu na urefu wa pande zake. Kuna kazi sita za trigonometriki kuhusiana na pembetatu ya pembe ya kulia.

p ni ya pembeni, h ni hypotenuse na b ni msingi wa pembe-kulia ∆ABC. ∆ ABC ni pembe ya kulia kwenye ncha B na θ ni pembe iliyo kinyume na upande uk.
Vitendaji sita vya trigonometric ni Sine (sin) , Cosine ( cos ), Tangent (tan ) , Cosecant (csc) , Secant (sec) , na Cotangent( cot) . Kazi tatu za mwisho zinalingana na zile tatu za kwanza.
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendicular ∕ Hypotenuse
\(\cos\theta = \) \(\frac{b}{h}\) = Msingi ∕ Hypotenuse
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendicular ∕ Msingi
Kwa hivyo \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Kwa hivyo, tunaweza kutumia trigonometry kupata pembe na pande zinazokosekana za pembetatu. Hebu tutumie utendaji wa trigonometric kutatua tatizo hapa chini.
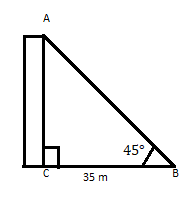
AC ni jengo ambalo juu yake hufanya angle ya 45 ° kwa umbali wa m 35 kutoka mguu wake kwenye ndege ya usawa. Tafuta urefu wa jengo.
Tunajua kwamba \(\tan\theta =\) Perpendicular (P) ∕ Base (B) , hapa \(\tan45=\frac{p}{35}\)
Tumia kikokotoo na uweke tu thamani ya pembe kwa digrii na ubonyeze kitufe cha "dhambi," "cos," au "tan". Au unaweza kutumia jedwali lililo hapa chini la uwiano wa Trigonometric kupata thamani ya \(\tan 45°\) .
| Kazi ya Trigonometric | 0° | 30° | 45° | 60° | 90° |
| dhambi | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| kitanda | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| sekunde | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Jedwali la uwiano wa trigonometric husaidia kupata thamani za pembe za kawaida za trigonometriki kama vile 0°, 30°, 45°, 60° na 90°. Inajumuisha uwiano wa trigonometric - sine, cosine, tangent, cosecant, secant, cotangent. Uwiano huu unaweza kuandikwa kwa ufupi kama sin, cos, tan, cosec, sec na cot. Thamani za uwiano wa trigonometric wa pembe za kawaida ni muhimu kutatua matatizo ya trigonometri. Kwa hiyo, ni muhimu kukumbuka maadili ya uwiano wa trigonometric wa pembe hizi za kawaida. Kuendelea na shida:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Jibu: urefu wa jengo ni 35 m.
Mzunguko wa Kitengo
Mduara wa kitengo una radius ya 1. Katikati ya duara imewekwa kwenye asili. Kwa hivyo urefu kutoka katikati hadi sehemu yoyote kwenye duara ni 1.

Kuratibu katika pointi nne ambapo mhimili hukutana na mduara ni (1,0), (0,1), (0,-1), (-1,0) . Ili kufanya pembe nzuri tunasonga kwa mwelekeo wa kinyume na kwa pembe hasi, tunatembea kwa mwelekeo wa saa. Hebu tuzingatie nukta iliyo na viwianishi (a,b) kwenye mduara baada ya kusogeza pembe θ kwa mwelekeo wa kinyume kutoka kwa mhimili wa x. P ni nukta kwenye duara yenye viwianishi (a,b). Pembetatu OPQ ni pembetatu ya pembe ya kulia kwa uhakika Q, yaani ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Tunaweza kuwakilisha kuratibu kwa uhakika P kama (cosθ, sinθ) . Kwa hivyo kosine ya θ ni sawa na viwianishi vya x ambapo upande wa mwisho wa pembe hukatiza mduara wa kitengo na sine ya θ ni sawa na viwianishi y ambapo upande wa mwisho wa pembe hukatiza mduara wa kitengo. Wacha tujaribu kutafuta thamani ya y kuratibu kwa uhakika A kwenye duara la kitengo hapa chini.

Jibu: Kuratibu Y kwa uhakika A ni \(\sin 270°\) .
Mduara wa kitengo huturuhusu kupanua kikoa cha sine na cosine hadi nambari zote halisi. Mchakato wa kuamua sine/kosini ya pembe yoyote θ ni kama ifuatavyo:
- Kuanzia (1,0) songa pamoja na mduara wa kitengo katika mwelekeo wa kinyume cha saa hadi pembe ambayo imeundwa kati ya nafasi yako, asili, na mhimili wa x chanya ni sawa na θ.
- \(\sin θ\) ni sawa na kiratibu cha y cha nukta yako, na \(\cos θ\) ni sawa na kiratibu cha x.
