ตรีโกณมิติเป็นสาขาหนึ่งของคณิตศาสตร์ที่ศึกษาความสัมพันธ์ระหว่างด้านและมุมของรูปสามเหลี่ยม ฟังก์ชันตรีโกณมิติเชื่อมโยงมุมของสามเหลี่ยมกับความยาวของด้าน มีฟังก์ชันตรีโกณมิติหกฟังก์ชันที่เกี่ยวข้องกับสามเหลี่ยมมุมฉาก
p ตั้งฉาก h คือด้านตรงข้ามมุมฉาก และ b เป็นฐานของมุมฉาก ∆ABC ∆ ABC เป็นมุมฉากที่จุด B และ θ เป็นมุมตรงข้ามกับด้าน p
ฟังก์ชันตรีโกณมิติทั้งหกคือ ไซน์
\(\sin\theta =\) \(\frac{p}{h}\) = ตั้งฉาก ∕ ด้านตรงข้ามมุมฉาก
\(\cos\theta = \) \(\frac{b}{h}\) = ฐาน ∕ ด้านตรงข้ามมุมฉาก
\(\tan\theta =\) \( \frac{p}{b}\) = ตั้งฉาก ∕ ฐาน
ดังนั้น \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
ดังนั้นเราจึงสามารถใช้ตรีโกณมิติเพื่อหามุมและด้านที่หายไปของรูปสามเหลี่ยมได้ ลองใช้ฟังก์ชันตรีโกณมิติเพื่อแก้ปัญหาด้านล่าง
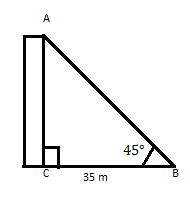
AC คืออาคารที่มียอดทำมุม 45° ที่ระยะ 35 ม. จากฐานบนระนาบแนวนอน ค้นหาความสูงของอาคาร
เรารู้ว่า \(\tan\theta =\) ตั้งฉาก
ใช้เครื่องคิดเลขและป้อนค่าของมุมเป็นองศา แล้วกดปุ่ม "sin" "cos" หรือ "tan" หรือคุณสามารถใช้ ตารางอัตราส่วนตรีโกณมิติ ด้านล่างเพื่อหาค่าของ \(\ tan \(\tan 45°\)
| ฟังก์ชันตรีโกณมิติ | 0° | 30° | 45° | 60° | 90° |
| บาป | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| เพราะ | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| ผิวสีแทน | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| เปล | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| โคเซก | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| วินาที | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
ตารางอัตราส่วนตรีโกณมิติ ช่วยในการหาค่าของมุมมาตรฐานตรีโกณมิติ เช่น 0°, 30°, 45°, 60° และ 90° ประกอบด้วยอัตราส่วนตรีโกณมิติ – ไซน์ โคไซน์ แทนเจนต์ โคซีแคนต์ ซีแคนต์ โคแทนเจนต์ อัตราส่วนเหล่านี้สามารถเขียนสั้นๆ เป็น sin, cos, tan, cosec, sec และ cot ค่าของอัตราส่วนตรีโกณมิติของมุมมาตรฐานมีความสำคัญต่อการแก้ปัญหาตรีโกณมิติ ดังนั้นจึง จำเป็นต้องจำค่าอัตราส่วนตรีโกณมิติของมุมมาตรฐานเหล่านี้ ดำเนินการต่อกับปัญหา:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
ตอบ ความสูงของอาคารคือ 35 ม.
วงกลมหนึ่งหน่วยมีรัศมีเป็น 1 จุดศูนย์กลางของวงกลมอยู่ที่จุดกำเนิด ดังนั้นความยาวจากจุดศูนย์กลางถึงจุดใดๆ บนวงกลมคือ 1
พิกัดที่สี่จุดที่แกนบรรจบวงกลมคือ (1,0), (0,1), (0,-1), (-1,0) ในการสร้างมุมบวก เราจะเคลื่อนที่ในทิศทางทวนเข็มนาฬิกา และสำหรับมุมลบ เราจะเคลื่อนที่ในทิศทางตามเข็มนาฬิกา ให้เราพิจารณาจุดที่มีพิกัด (a,b) บนวงกลมหลังจากเคลื่อนที่เป็นมุม θ ในทิศทางทวนเข็มนาฬิกาจากแกน x P คือจุดบนวงกลมที่มีพิกัด (a,b) สามเหลี่ยม OPQ เป็นรูปสามเหลี่ยมมุมฉากที่จุด Q นั่นคือ ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
เราสามารถแสดงพิกัดที่จุด P เป็น (cosθ, sinθ) . โคไซน์ของ θ เท่ากับพิกัด x โดยที่ด้านปลายของมุมตัดกับวงกลมหน่วย และไซน์ของ θ เท่ากับพิกัด y โดยที่ด้านปลายของมุมตัดกับวงกลมหน่วย ลองหาค่าพิกัด y ที่จุด A ในวงกลมหน่วยด้านล่างกัน
คำตอบ: พิกัด Y ที่จุด A คือ \(\sin 270°\)
วงกลมหน่วยช่วยให้เราสามารถขยายโดเมนของไซน์และโคไซน์ไปยังจำนวนจริงทั้งหมดได้ กระบวนการหาค่าไซน์/โคไซน์ของมุมใดๆ θ มีดังต่อไปนี้:
