Ang trigonometrya ay isang sangay ng matematika na nag-aaral ng ugnayan sa pagitan ng mga gilid at anggulo ng isang tatsulok. Iniuugnay ng mga function ng trigonometriko ang anggulo ng isang tatsulok sa haba ng mga gilid nito. Mayroong anim na trigonometric function na may kaugnayan sa right angle triangle.
p ay patayo, h ang hypotenuse at b ang base ng right-angle ∆ABC. Ang ∆ ABC ay isang tamang anggulo sa punto B at ang θ ay ang anggulo sa tapat ng gilid p.
Ang anim na trigonometric function ay Sine
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendicular ∕ Hypotenuse
\(\cos\theta = \) \(\frac{b}{h}\) = Base ∕ Hypotenuse
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendikular ∕ Base
Samakatuwid \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Kaya, maaari nating gamitin ang trigonometry upang mahanap ang mga nawawalang anggulo at gilid ng isang tatsulok. Mag-apply tayo ng trigonometric function upang malutas ang problema sa ibaba.
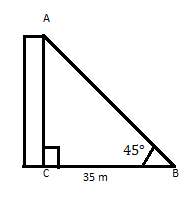
Ang AC ay isang gusali na ang tuktok ay gumagawa ng isang anggulo na 45° sa layo na 35 m mula sa paa nito sa isang pahalang na eroplano. Hanapin ang taas ng gusali.
Alam namin na \(\tan\theta =\) Perpendicular
Gumamit ng calculator at ipasok lamang ang halaga ng anggulo sa mga degree at itulak ang "sin," "cos," o "tan" na button. O maaari mong gamitin ang talahanayan sa ibaba ng Trigonometric ratios upang mahanap ang halaga ng \(\tan 45°\) .
| Trigonometric Function | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | ∞ | \(\sqrt3\) | 1 |
| \(\sqrt3\) | frac | \(\frac{1}{\sqrt3}\) | 0 | cosec | ∞ |
| \ | sqrt3 | \ | \(\sqrt2 \) | \(2/\sqrt3\) | ( |
| \ | sqrt2 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Tinutulungan ng talahanayan ng trigonometric ratios na mahanap ang mga halaga ng mga karaniwang anggulo ng trigonometriko gaya ng 0°, 30°, 45°, 60° at 90°. Binubuo ito ng trigonometric ratios - sine, cosine, tangent, cosecant, secant, cotangent. Ang mga ratio na ito ay maaaring isulat sa madaling salita bilang sin, cos, tan, cosec, sec at cot. Ang mga halaga ng trigonometric ratios ng mga karaniwang anggulo ay mahalaga upang malutas ang mga problema sa trigonometry. Samakatuwid, kinakailangang tandaan ang mga halaga ng trigonometriko ratios ng mga karaniwang anggulong ito. Pagpapatuloy sa problema:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Sagot: Ang taas ng gusali ay 35 m.
Ang unit circle ay may radius na 1. Ang gitna ng bilog ay inilalagay sa pinanggalingan. Kaya ang haba mula sa gitna hanggang sa anumang punto sa bilog ay 1.
Ang mga coordinate sa apat na punto kung saan ang axis ay nakakatugon sa bilog ay (1,0), (0,1), (0,-1), (-1,0). Upang makagawa ng positibong anggulo, gumagalaw tayo sa pakaliwa na direksyon at para sa negatibong anggulo, gumagalaw tayo sa direksyong pakanan. Isaalang-alang natin ang isang punto na may mga coordinate (a,b) sa isang bilog pagkatapos ilipat ang anggulo θ sa pakaliwa na direksyon mula sa x-axis. Ang P ay isang punto sa bilog na may mga coordinate (a,b). Ang Triangle OPQ ay isang right angle triangle sa point Q, ibig sabihin, ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Maaari naming katawanin ang mga coordinate sa punto P bilang (cosθ, sinθ) . Kaya ang cosine ng θ ay katumbas ng x coordinate kung saan ang terminal na bahagi ng anggulo ay bumalandra sa unit circle at ang sine ng θ ay katumbas ng y coordinate kung saan ang terminal side ng anggulo ay intersects sa unit circle. Subukan nating hanapin ang halaga ng y coordinate sa punto A sa ibaba ng bilog na yunit.
Sagot: Ang Y coordinate sa punto A ay \(\sin 270°\) .
Ang bilog ng yunit ay nagpapahintulot sa amin na palawigin ang domain ng sine at cosine sa lahat ng tunay na numero. Ang proseso para sa pagtukoy ng sine/cosine ng anumang anggulo θ ay ang mga sumusunod: