Trigonometri, bir üçgenin kenarları ve açıları arasındaki ilişkiyi inceleyen bir matematik dalıdır. Trigonometrik fonksiyonlar, bir üçgenin açısını kenarlarının uzunluğuyla ilişkilendirir. Dik açılı üçgene bağlı olarak altı trigonometrik fonksiyon vardır.

p diktir, h hipotenüstür ve b ∆ABC dik açısının tabanıdır. ∆ ABC, B noktasında bir dik açıdır ve θ, p kenarının karşısındaki açıdır.
Altı trigonometrik fonksiyon Sinüs (sin) , Kosinüs ( cos ), Tanjant (tan ) , Cosekant (csc) , Secant (sec) ve Cotangent( cot) şeklindedir. Son üç fonksiyon, ilk üç fonksiyonun tersidir.
\(\sin\theta =\) \(\frac{p}{h}\) = Dik ∕ Hipotenüs
\(\cos\theta = \) \(\frac{b}{h}\) = Taban ∕ Hipotenüs
\(\tan\theta =\) \( \frac{p}{b}\) = Dikey ∕ Taban
Bu nedenle \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Bu nedenle, bir üçgenin eksik açılarını ve kenarlarını bulmak için trigonometriyi kullanabiliriz. Aşağıdaki problemi çözmek için bir trigonometrik fonksiyon uygulayalım.
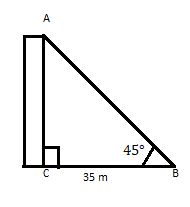
AC, yatay düzlemde ayağından 35 m uzaklıkta tepesi 45° açı yapan bir yapıdır. Binanın yüksekliğini bulun.
Biliyoruz ki \(\tan\theta =\) Dik (P) ∕ Taban (B) , burada \(\tan45=\frac{p}{35}\)
Bir hesap makinesi kullanın ve açının değerini derece olarak girin ve "sin", "cos" veya "tan" düğmesine basın. Veya \(\tan 45°\) değerini bulmak için aşağıdaki Trigonometrik oranlar tablosunu kullanabilirsiniz .
| Trigonometrik fonksiyon | 0° | 30° | 45° | 60° | 90° |
| günah | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| çünkü | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| bronzlaşmak | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| karyola | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| kosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| saniye | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Trigonometrik oranlar tablosu, 0°, 30°, 45°, 60° ve 90° gibi trigonometrik standart açıların değerlerini bulmaya yardımcı olur. Trigonometrik oranlardan oluşur - sinüs, kosinüs, teğet, kosekant, sekant, kotanjant. Bu oranlar kısaca sin, cos, tan, cosec, sec ve cot olarak yazılabilir. Standart açıların trigonometrik oranlarının değerleri, trigonometri problemlerini çözmek için gereklidir. Bu nedenle, bu standart açıların trigonometrik oranlarının değerlerini hatırlamak gerekir. Soruna devam etmek:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Cevap: Binanın yüksekliği 35 m'dir.
Birim çember
Bir birim çemberin yarıçapı 1'dir. Çemberin merkezi orijindedir. Yani merkezden daire üzerindeki herhangi bir noktaya olan uzunluk 1'dir.

Eksenin çemberle birleştiği dört noktadaki koordinatlar (1,0), (0,1), (0,-1), (-1,0) şeklindedir. Pozitif açı yapmak için saat yönünün tersine, negatif açı yapmak için saat yönünde hareket ederiz. Bir daire üzerinde (a,b) koordinatlarına sahip bir noktayı x ekseninden saat yönünün tersine θ açısını hareket ettirdikten sonra ele alalım. P, daire üzerinde koordinatları (a,b) olan bir noktadır. Üçgen OPQ, Q noktasında dik açılı bir üçgendir, yani ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
P noktasındaki koordinatları (cosθ, sinθ) olarak gösterebiliriz . Yani θ'nın kosinüsü, açının terminal tarafının birim çemberle kesiştiği x koordinatlarına ve θ'nın sinüsü, açının terminal tarafının birim çemberle kesiştiği yerde y koordinatlarına eşittir. Aşağıdaki birim çemberde A noktasındaki y koordinatının değerini bulmaya çalışalım.

Cevap: A noktasındaki Y koordinatı \(\sin 270°\) dir.
Birim çember, sinüs ve kosinüs alanını tüm gerçek sayılara genişletmemizi sağlar. Herhangi bir θ açısının sinüs/kosinüsünü belirleme işlemi aşağıdaki gibidir:
- (1,0)'dan başlayarak, konumunuz, orijin ve pozitif x ekseni arasında oluşan açı θ'ya eşit olana kadar birim çember boyunca saat yönünün tersine hareket edin.
- \(\sin θ\) noktanızın y koordinatına ve \(\cos θ\) x koordinatına eşittir.
