Тригонометрія — це розділ математики, який вивчає співвідношення між сторонами та кутами трикутника. Тригонометричні функції зв’язують кут трикутника з довжиною його сторін. Є шість тригонометричних функцій по відношенню до прямокутного трикутника.
p — перпендикуляр, h — гіпотенуза, b — основа прямокутника ∆ABC. ∆ ABC — прямий кут у точці B, а θ — кут, протилежний стороні p.
Шість тригонометричних функцій є синусом
\(\sin\theta =\) \(\frac{p}{h}\) = перпендикуляр ∕ гіпотенуза
\(\cos\theta = \) \(\frac{b}{h}\) = основа ∕ гіпотенуза
\(\tan\theta =\) \( \frac{p}{b}\) = перпендикуляр ∕ основа
Тому \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Отже, ми можемо використовувати тригонометрію, щоб знайти відсутні кути та сторони трикутника. Давайте застосуємо тригонометричну функцію, щоб розв’язати наведену нижче задачу.
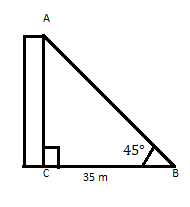
АС — будівля, вершина якої на відстані 35 м від її підніжжя на горизонтальній площині утворює кут 45°. Знайдіть висоту будівлі.
Ми знаємо, що \(\tan\theta =\) перпендикуляр
Скористайтеся калькулятором і просто введіть значення кута в градусах і натисніть кнопку «sin», «cos» або «tan». Або ви можете скористатися наведеною нижче таблицею тригонометричних співвідношень , щоб знайти значення \(\tan 45°\) .
| Тригонометрична функція | 0° | 30° | 45° | 60° | 90° |
| гріх | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| загар | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| ліжечко | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| сек | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Таблиця тригонометричних співвідношень допомагає знайти значення тригонометричних стандартних кутів, таких як 0°, 30°, 45°, 60° і 90°. Він складається з тригонометричних співвідношень – синуса, косинуса, тангенса, косекансу, секансу, котангенса. Ці співвідношення можна коротко записати як sin, cos, tan, cosec, sec і cot. Значення тригонометричних відношень стандартних кутів необхідні для розв’язування задач тригонометрії. Тому необхідно запам'ятати значення тригонометричних співвідношень цих стандартних кутів. Продовжуючи проблему:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Відповідь: Висота будівлі 35 м.
Одиничне коло має радіус 1. Центр кола знаходиться в початку координат. Отже, довжина від центру до будь-якої точки кола дорівнює 1.
Координати в чотирьох точках, де вісь перетинає коло, дорівнюють (1,0), (0,1), (0,-1), (-1,0) . Щоб отримати позитивний кут, ми рухаємося проти годинникової стрілки, а для від’ємного кута рухаємося за годинниковою стрілкою. Розглянемо точку з координатами (a,b) на колі після переміщення кута θ проти годинникової стрілки від осі x. P — точка на колі з координатами (a,b). Трикутник OPQ — прямокутний трикутник у точці Q, тобто ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Ми можемо представити координати в точці P як (cosθ, sinθ) . Отже, косинус θ дорівнює координатам x, де кінцева сторона кута перетинає одиничне коло, а синус θ дорівнює координатам y, де кінцева сторона кута перетинає одиничне коло. Давайте спробуємо знайти значення координати y у точці А в одиничному колі нижче.
Відповідь: Координата Y у точці А дорівнює \(\sin 270°\) .
Одиничне коло дозволяє розширити область визначення синуса і косинуса на всі дійсні числа. Процес визначення синуса/косинуса будь-якого кута θ виглядає наступним чином: