مثلثیات ریاضی کی ایک شاخ ہے جو مثلث کے اطراف اور زاویوں کے درمیان تعلق کا مطالعہ کرتی ہے۔ مثلثی افعال مثلث کے زاویہ کو اس کے اطراف کی لمبائی سے جوڑتے ہیں۔ دائیں زاویہ مثلث کے سلسلے میں چھ مثلثیاتی افعال ہیں۔
p کھڑا ہے، h hypotenuse ہے اور b دائیں زاویہ ∆ABC کی بنیاد ہے۔ ∆ ABC نقطہ B پر ایک دائیں زاویہ ہے اور θ طرف p کے مخالف زاویہ ہے۔
چھ مثلثی افعال Sine ہیں۔
\(\sin\theta =\) \(\frac{p}{h}\) = کھڑا ∕ Hypotenuse
\(\cos\theta = \) \(\frac{b}{h}\) = بنیاد ∕ ہائپوٹینوز
\(\tan\theta =\) \( \frac{p}{b}\) = کھڑا ∕ بنیاد
لہذا \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
لہذا، ہم مثلث کے گمشدہ زاویوں اور اطراف کو تلاش کرنے کے لیے مثلثیات کا استعمال کر سکتے ہیں۔ آئیے ذیل میں مسئلے کو حل کرنے کے لیے ایک مثلثی فنکشن کا اطلاق کریں۔
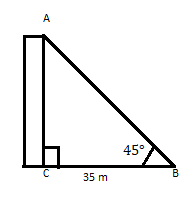
AC ایک عمارت ہے جس کی چوٹی افقی جہاز پر اپنے پاؤں سے 35 میٹر کے فاصلے پر 45° کا زاویہ بناتی ہے۔ عمارت کی اونچائی تلاش کریں۔
ہم جانتے ہیں کہ \(\tan\theta =\) کھڑا
ایک کیلکولیٹر استعمال کریں اور زاویہ کی قدر کو ڈگری میں داخل کریں اور "sin," "cos" یا "tan" بٹن کو دبائیں۔ یا آپ \(\tan 45°\) کی قدر معلوم کرنے کے لیے نیچے کی مثلثی تناسب کی جدول استعمال کر سکتے ہیں ۔
| ٹرگنومیٹرک فنکشن | 0° | 30° | 45° | 60° | 90° |
| گناہ | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| ٹین | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| پلنگ | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| سیکنڈ | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
مثلثی تناسب کا جدول مثلثی معیاری زاویوں جیسے 0°، 30°، 45°، 60° اور 90° کی قدریں تلاش کرنے میں مدد کرتا ہے۔ یہ مثلثی تناسب پر مشتمل ہوتا ہے - سائن، کوزائن، ٹینجنٹ، کوسیکینٹ، سیکینٹ، کوٹینجینٹ۔ ان تناسب کو sin، cos، tan، cosec، sec اور cot کے طور پر مختصراً لکھا جا سکتا ہے۔ معیاری زاویوں کے مثلثی تناسب کی قدریں مثلثیات کے مسائل کو حل کرنے کے لیے ضروری ہیں۔ لہذا، ان معیاری زاویوں کے مثلثی تناسب کی قدروں کو یاد رکھنا ضروری ہے۔ مسئلہ کو جاری رکھنا:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
جواب: عمارت کی اونچائی 35 میٹر ہے۔
ایک یونٹ کے دائرے کا رداس 1 ہے۔ دائرے کا مرکز اصل میں رکھا گیا ہے۔ تو مرکز سے دائرے کے کسی بھی نقطہ تک لمبائی 1 ہے۔
چار پوائنٹس پر محور جہاں محور دائرے سے ملتا ہے وہ ہیں (1,0), (0,1), (0,-1), (-1,0)۔ مثبت زاویہ بنانے کے لیے ہم گھڑی کی مخالف سمت میں حرکت کرتے ہیں اور منفی زاویہ کے لیے ہم گھڑی کی سمت میں حرکت کرتے ہیں۔ آئیے ہم زاویہ θ کو ایکس محور سے مخالف گھڑی کی سمت میں منتقل کرنے کے بعد دائرے پر نقاط (a,b) کے ساتھ ایک نقطہ پر غور کریں۔ P نقاط (a,b) کے ساتھ دائرے پر ایک نقطہ ہے۔ مثلث OPQ نقطہ Q پر ایک دائیں زاویہ مثلث ہے، یعنی ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
ہم پوائنٹ P پر نقاط کو بطور (cosθ, sinθ) پیش کر سکتے ہیں ۔ لہذا θ کا کوسائن x کوآرڈینیٹ کے برابر ہے جہاں زاویہ کا ٹرمینل سائیڈ یونٹ کے دائرے کو کاٹتا ہے اور θ کی سائن y کوآرڈینیٹ کے برابر ہے جہاں زاویہ کا ٹرمینل سائیڈ یونٹ کے دائرے کو کاٹتا ہے۔ آئیے نیچے یونٹ کے دائرے میں پوائنٹ A پر y کوآرڈینیٹ کی قدر تلاش کرنے کی کوشش کرتے ہیں۔
جواب: پوائنٹ A پر Y کوآرڈینیٹ ہے \(\sin 270°\) ۔
یونٹ کا دائرہ ہمیں سائن اور کوزائن کے ڈومین کو تمام حقیقی نمبروں تک بڑھانے کی اجازت دیتا ہے۔ کسی بھی زاویہ θ کی سائن/کوزائن کا تعین کرنے کا عمل درج ذیل ہے: