Trigonometriya uchburchakning tomonlari va burchaklari oʻrtasidagi bogʻliqlikni oʻrganuvchi matematikaning boʻlimidir. Trigonometrik funktsiyalar uchburchakning burchagini uning tomonlari uzunligi bilan bog'laydi. To'g'ri burchakli uchburchakka nisbatan oltita trigonometrik funktsiya mavjud.
p - perpendikulyar, h - gipotenuza va b - ∆ABC to'g'ri burchakli burchakning asosi. ∆ ABC - B nuqtadagi to'g'ri burchak va th - p tomoniga qarama-qarshi burchak.
Oltita trigonometrik funksiyalar sinus
\(\sin\theta =\) \(\frac{p}{h}\) = Perpendikulyar ∕ Gipotenuza
\(\cos\theta = \) \(\frac{b}{h}\) = Baza ∕ Gipotenuza
\(\tan\theta =\) \( \frac{p}{b}\) = Perpendikulyar ∕ asos
Shuning uchun \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Shunday qilib, biz uchburchakning etishmayotgan burchaklari va tomonlarini topish uchun trigonometriyadan foydalanishimiz mumkin. Quyidagi masalani yechish uchun trigonometrik funktsiyani qo'llaymiz.
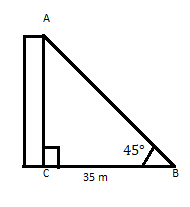
AC - gorizontal tekislikdagi oyog'idan 35 m masofada tepasi 45 ° burchak ostida bo'lgan bino. Binoning balandligini toping.
Biz bilamizki, \(\tan\theta =\) Perpendikulyar
Kalkulyatordan foydalaning va burchak qiymatini darajalarda kiriting va "sin", "cos" yoki "tan" tugmasini bosing. Yoki \(\tan 45°\) qiymatini topish uchun quyidagi Trigonometrik nisbatlar jadvalidan foydalanishingiz mumkin .
| Trigonometrik funksiya | 0° | 30° | 45° | 60° | 90° |
| sin | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| tan | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| beshik | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| kosek | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| soniya | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Trigonometrik nisbatlar jadvali 0°, 30°, 45°, 60° va 90° kabi trigonometrik standart burchaklarning qiymatlarini topishga yordam beradi. U trigonometrik nisbatlardan iborat - sinus, kosinus, tangens, kosekant, sekant, kotangent. Bu nisbatlarni sin, cos, tan, kosek, sek va kot kabi qisqacha yozish mumkin. Standart burchaklarning trigonometrik nisbatlarining qiymatlari trigonometriya masalalarini yechish uchun zarurdir. Shuning uchun bu standart burchaklarning trigonometrik nisbatlarining qiymatlarini eslab qolish kerak. Muammoni davom ettirish:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Javob: Binoning balandligi 35 m.
Birlik aylana radiusi 1 ga teng. Aylananing markazi koordinata boshida joylashgan. Shunday qilib, markazdan aylananing istalgan nuqtasigacha bo'lgan uzunlik 1 ga teng.
Eksa aylana bilan uchrashadigan to'rtta nuqtadagi koordinatalar (1,0), (0,1), (0,-1), (-1,0) dir. Ijobiy burchak hosil qilish uchun biz soat miliga teskari yo'nalishda harakat qilamiz va salbiy burchak uchun soat yo'nalishi bo'yicha harakat qilamiz. th burchakni x o'qidan soat miliga teskari yo'nalishda harakatlantirgandan so'ng aylana ustidagi koordinatalari (a,b) bo'lgan nuqtani ko'rib chiqaylik. P - koordinatalari (a,b) bo'lgan doiradagi nuqta. OPQ uchburchagi Q nuqtadagi to‘g‘ri burchakli uchburchakdir, ya’ni ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
P nuqtadagi koordinatalarni (costh, sinth) shaklida ifodalashimiz mumkin . Demak, th ning kosinasi x koordinatalariga teng, bu erda burchakning oxirgi tomoni birlik doirasini kesib o'tadi va th sinusi burchakning terminal tomoni birlik doirasini kesib o'tadigan y koordinatalariga teng. Quyidagi birlik doiradagi A nuqtadagi y koordinatasining qiymatini topishga harakat qilaylik.
Javob: A nuqtadagi Y koordinatasi \(\sin 270°\) ga teng.
Birlik doirasi sinus va kosinus sohasini barcha haqiqiy sonlarga kengaytirish imkonini beradi. Har qanday th burchakning sinusi/kosinusini aniqlash jarayoni quyidagicha: