Lượng giác là một nhánh của toán học nghiên cứu mối quan hệ giữa các cạnh và các góc của một tam giác. Các hàm lượng giác liên hệ góc của một tam giác với độ dài các cạnh của nó. Có sáu hàm lượng giác liên quan đến tam giác vuông góc.
p vuông góc, h là cạnh huyền và b là đáy của góc vuông ∆ABC. ∆ ABC vuông tại điểm B và θ là góc đối với cạnh p.
Sáu hàm lượng giác là Sin
\(\sin\theta =\) \(\frac{p}{h}\) = Vuông góc ∕ Cạnh huyền
\(\cos\theta = \) \(\frac{b}{h}\) = Cơ sở ∕ Cạnh huyền
\(\tan\theta =\) \( \frac{p}{b}\) = Vuông góc ∕ Cơ sở
Do đó \( \tan\theta = \frac{\sin\theta}{\cos\theta}\)
\(\csc\theta = \frac{1}{\sin\theta} =\) \( \frac{h}{p}\)
\(\sec\theta = \frac{1}{\cos\theta} =\) \(\frac{h}{b}\)
\(\cot\theta = \frac{1}{\tan\theta} = \) \(\frac{b}{p}\)
Do đó, chúng ta có thể sử dụng lượng giác để tìm các góc và các cạnh còn thiếu của một tam giác. Hãy áp dụng một hàm lượng giác để giải bài toán dưới đây.
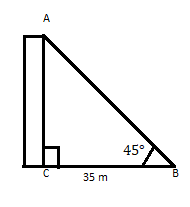
AC là một tòa nhà có đỉnh tạo với góc 45° ở khoảng cách 35 m so với chân của nó trên mặt phẳng nằm ngang. Tìm chiều cao của tòa nhà.
Chúng tôi biết rằng \(\tan\theta =\) Vuông góc
Sử dụng máy tính và chỉ cần nhập giá trị của góc theo độ và nhấn nút "sin", "cos" hoặc "tan". Hoặc bạn có thể sử dụng bảng tỷ lệ lượng giác bên dưới để tìm giá trị của \(\tan 45°\) .
| hàm lượng giác | 0° | 30° | 45° | 60° | 90° |
| tội | 0 | 1/2 | \(\sqrt2/2\) | \(\sqrt3/2\) | 1 |
| cos | 1 | \(\sqrt3/2\) | \(\sqrt2/2\) | 1/2 | 0 |
| rám nắng | 0 | \(\sqrt3/3\) | 1 | \(\sqrt3\) | ∞ |
| cũi | ∞ | \(\sqrt3\) | 1 | \(\frac{1}{\sqrt3}\) | 0 |
| cosec | ∞ | 2 | \(\sqrt2 \) | \(2/\sqrt3\) | 1 |
| giây | 1 | \(2/\sqrt3\) | \(\sqrt2 \) | 2 | ∞ |
Bảng tỉ số lượng giác giúp tìm giá trị của các góc chuẩn lượng giác như 0°, 30°, 45°, 60° và 90°. Nó bao gồm các tỷ số lượng giác – sin, cosin, tangent, cosecant, secant, cotang. Các tỷ lệ này có thể được viết ngắn gọn là sin, cos, tan, cosec, sec và cot. Giá trị của các tỉ số lượng giác của các góc chuẩn rất cần thiết để giải các bài toán lượng giác. Vì vậy cần nhớ giá trị các tỉ số lượng giác của các góc chuẩn này. Tiếp tục vấn đề:
\(\therefore \tan 45 = 1 = \frac{p}{35} \)
\(p = 35\)
Trả lời: Chiều cao của tòa nhà là 35 m.
Một đường tròn đơn vị có bán kính là 1. Tâm của đường tròn được đặt ở gốc tọa độ. Vì vậy, độ dài từ tâm đến bất kỳ điểm nào trên đường tròn là 1.
Tọa độ tại bốn điểm mà trục gặp đường tròn là (1,0), (0,1), (0,-1), (-1,0) . Để tạo một góc dương, chúng ta di chuyển theo hướng ngược chiều kim đồng hồ và đối với một góc âm, chúng ta di chuyển theo chiều kim đồng hồ. Chúng ta hãy xem xét một điểm có tọa độ (a, b) trên một đường tròn sau khi di chuyển góc θ theo hướng ngược chiều kim đồng hồ từ trục x. P là một điểm trên đường tròn có tọa độ (a,b). Tam giác OPQ là tam giác vuông tại điểm Q, nghĩa là ∠ PQO = 90°
\(\cos\theta = \frac{a}{1}\)
\(\sin\theta = \frac{b}{1}\)
\(\tan\theta = \frac{b}{a}\)
Ta có thể biểu diễn tọa độ tại điểm P là (cosθ, sinθ) . Vì vậy, cosin của θ bằng tọa độ x trong đó cạnh cuối của góc cắt đường tròn đơn vị và sin của θ bằng tọa độ y trong đó cạnh cuối của góc cắt đường tròn đơn vị. Hãy thử tìm giá trị của tọa độ y tại điểm A trong vòng tròn đơn vị bên dưới.
Trả lời: Tọa độ Y tại điểm A là \(\sin 270°\) .
Đường tròn đơn vị cho phép ta mở rộng miền sin và cosin cho mọi số thực. Quy trình xác định sin/cosin của bất kỳ góc θ nào như sau: