إذا كان اليوم هو الأحد فمن المؤكد أن يكون غدًا الاثنين. من المؤكد أن الشمس ستشرق من الشرق. ومن المستحيل أيضًا أن تنمو أطول من الزرافة. بالنسبة لبعض الأحداث، نحن متأكدون من النتيجة. لكن فكر في الموقف الذي تتنافس فيه مع ثمانية متسابقين آخرين للفوز بالسباق. قد تفوز بالسباق لكن الأمر غير مؤكد. عند شراء تذكرة اليانصيب، قد تفوز. ولكن نظرًا لأن عددًا كبيرًا من الأشخاص قد اشتروا التذاكر لنفس اليانصيب، فإن فرص فوزك أقل جدًا.
تسمى فرص وقوع حدث ما عند قياسها كميا بالاحتمال. يستخدم الاحتمال الأرقام لقياس فرصة حدوث نتيجة ما. يمكن إظهار احتمالية النتيجة باستخدام المقياس أدناه:
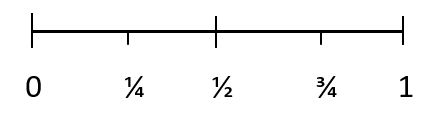
جميع الاحتمالات لها قيمة بين 0 و1. احتمال النتيجة المستحيلة هو 0. واحتمال نتيجة معينة هو 1. 1/4 يمثل حدثًا غير محتمل الحدوث، 1/2 يمثل فرصة زوجية لحدوث شيء ما الحدث و3/4 يمثل حدثًا محتمل الحدوث.
دعونا نضع علامة على كل من هذه النتائج على مقياس الاحتمالية:
يتم تعريف احتمال حدوث الحدث E، المشار إليه بـ P(E)، على أنه
\(P(E) =\frac{\textrm{عدد النتائج الإيجابية}}{\textrm{العدد الإجمالي للنتائج المحتملة}} = \frac{e}{n}\)
حيث تكون النتيجة نتيجة التجربة. والنتيجة الإيجابية هي ذلك الحدث الذي نرغب في تحديد احتمالية حدوثه.
دعونا نتعلم الاحتمال مع بعض الأمثلة:
1) إذا تم سحب بطاقة من مجموعة مكونة من 52 بطاقة تم خلطها جيدًا، ما هو احتمال سحب ملكة؟
الحل: إجمالي عدد النتائج المحتملة = 52
هناك 4 ملكات في مجموعة مكونة من 52 بطاقة ويمكن سحب أي ملكة.
وبالتالي فإن عدد النتائج الإيجابية = 4
احتمال سحب الملكة هو \(\frac{4}{52} = \frac{1}{13}\)
2) ما هو احتمال الحصول على عدد زوجي عند رمي حجر النرد؟
الحل: إجمالي عدد النتائج = 6
إجمالي عدد النتائج الإيجابية = 3 (الأرقام الزوجية هي 2 و4 و6)
وبالتالي، فإن احتمال الحصول على رقم زوجي هو \(\frac{3}{6} = \frac{1}{2}\)