আজ রবিবার না হলে আগামীকাল সোমবার হওয়া নিশ্চিত। সূর্য অবশ্যই পূর্ব দিকে উঠবে। এছাড়াও, এটা অসম্ভব যে আপনি জিরাফের চেয়ে লম্বা হবেন। কয়েকটি ঘটনার জন্য, আমরা ফলাফল সম্পর্কে নিশ্চিত। কিন্তু পরিস্থিতির কথা চিন্তা করুন যেখানে আপনি দৌড়ে জয়ী হওয়ার জন্য অন্য আটজন দৌড়বিদদের সাথে প্রতিযোগিতা করছেন। আপনি দৌড়ে জিততে পারেন তবে এটি নিশ্চিত নয়। আপনি যখন একটি লটারির টিকিট কিনবেন, আপনি জিততে পারেন। কিন্তু যেহেতু লক্ষ লক্ষ লোক একই লটারির জন্য টিকিট কিনেছে, তাই আপনার জেতার সম্ভাবনা খুবই কম।
পরিমাণগতভাবে পরিমাপ করা হলে ঘটনা ঘটার সম্ভাবনা বলা হয় সম্ভাব্যতা। সম্ভাব্যতা একটি ফলাফল ঘটার সম্ভাবনা পরিমাপ করতে সংখ্যা ব্যবহার করে। একটি ফলাফলের সম্ভাবনা নীচের স্কেল ব্যবহার করে দেখানো যেতে পারে:
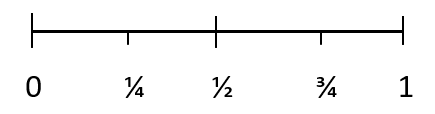
সমস্ত সম্ভাব্যতার একটি মান 0 এবং 1 এর মধ্যে রয়েছে। একটি অসম্ভব ফলাফলের সম্ভাবনা হল 0। এবং একটি নির্দিষ্ট ফলাফলের সম্ভাব্যতা হল 1। 1/4 এমন একটি ঘটনাকে উপস্থাপন করে যা ঘটতে পারে না, 1/2 একটি ঘটনা ঘটার সম্ভাবনাকে প্রতিনিধিত্ব করে। ঘটনা এবং 3/4 ঘটতে পারে এমন একটি ঘটনাকে উপস্থাপন করে।
আসুন সম্ভাব্যতার স্কেলে এই প্রতিটি ফলাফলকে চিহ্নিত করি:
P(E) দ্বারা নির্দেশিত একটি ইভেন্ট E ঘটার সম্ভাবনা হিসাবে সংজ্ঞায়িত করা হয়
\(P(E) =\frac{\textrm{অনুকূল ফলাফলের সংখ্যা}}{\textrm{সম্ভাব্য ফলাফলের মোট সংখ্যা}} = \frac{e}{n}\)
যেখানে ফলাফল পরীক্ষার ফলাফল। একটি অনুকূল ফলাফল হল সেই ঘটনা যার সংঘটনের সম্ভাব্যতা আমরা নির্ধারণ করতে চাই।
আসুন কয়েকটি উদাহরণ দিয়ে সম্ভাব্যতা শিখি:
1) যদি 52টি কার্ডের একটি ভালভাবে এলোমেলো ডেক থেকে একটি কার্ড আঁকা হয়, তাহলে একটি রানী আঁকার সম্ভাবনা কত?
সমাধান: সম্ভাব্য ফলাফলের মোট সংখ্যা = 52
52টি কার্ডের একটি ডেকে 4টি রানী রয়েছে এবং যে কেউ রানী আঁকা যেতে পারে।
অতএব, অনুকূল ফলাফলের সংখ্যা = 4
রাণী আঁকার সম্ভাবনা হল \(\frac{4}{52} = \frac{1}{13}\)
2) একটি পাশা নিক্ষেপ করা হলে একটি জোড় সংখ্যা পাওয়ার সম্ভাবনা কত?
সমাধান: মোট ফলাফলের সংখ্যা = 6
অনুকূল ফলাফলের মোট সংখ্যা = 3 (জোড় সংখ্যা হল 2, 4 এবং 6)
অতএব, একটি জোড় সংখ্যা পাওয়ার সম্ভাবনা হল \(\frac{3}{6} = \frac{1}{2}\)