Wenn heute Sonntag ist, ist es sicher, dass morgen Montag ist. Die Sonne wird sicherlich im Osten aufgehen. Außerdem ist es unmöglich, größer als eine Giraffe zu werden. Bei einigen Ereignissen sind wir uns über den Ausgang sicher. Aber stellen Sie sich die Situation vor, in der Sie mit acht anderen Läufern um den Sieg konkurrieren. Sie können das Rennen gewinnen, aber es ist nicht sicher. Wenn Sie einen Lottoschein kaufen, können Sie gewinnen. Aber da viele Leute die Lose für die gleiche Lotterie gekauft haben, sind Ihre Gewinnchancen sehr gering.
Die quantitativ gemessene Wahrscheinlichkeit des Eintretens eines Ereignisses wird als Wahrscheinlichkeit bezeichnet. Die Wahrscheinlichkeit verwendet Zahlen, um die Wahrscheinlichkeit zu messen, dass ein Ergebnis eintritt. Die Wahrscheinlichkeit eines Ergebnisses kann anhand der folgenden Skala dargestellt werden:
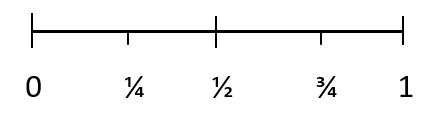
Alle Wahrscheinlichkeiten haben einen Wert zwischen 0 und 1. Die Wahrscheinlichkeit eines unmöglichen Ergebnisses ist 0. Und die Wahrscheinlichkeit eines bestimmten Ergebnisses ist 1. 1/4 stellt ein Ereignis dar, dessen Eintritt unwahrscheinlich ist, 1/2 stellt eine gerade Chance für das Eintreten eines Ereignisses dar Ereignis und 3/4 stellt ein Ereignis dar, das wahrscheinlich eintreten wird.
Markieren wir jedes dieser Ergebnisse auf einer Wahrscheinlichkeitsskala:
Die Wahrscheinlichkeit des Eintretens eines Ereignisses E, bezeichnet mit P(E), ist definiert als
\(P(E) =\frac{\textrm{Anzahl günstiger Ergebnisse}}{\textrm{Gesamtzahl der möglichen Ergebnisse}} = \frac{e}{n}\)
wobei das Ergebnis ein Ergebnis des Experiments ist. Ein günstiger Ausgang ist das Ereignis, dessen Eintrittswahrscheinlichkeit wir bestimmen wollen.
Lassen Sie uns die Wahrscheinlichkeit anhand einiger Beispiele lernen:
1) Wie groß ist die Wahrscheinlichkeit, eine Dame zu ziehen, wenn eine Karte aus einem gut gemischten Kartenspiel mit 52 Karten gezogen wird?
Lösung: Gesamtzahl der möglichen Ergebnisse = 52
Es gibt 4 Damen in einem Kartenspiel mit 52 Karten und es kann jede Königin gezogen werden.
Daher ist die Anzahl der günstigen Ergebnisse = 4
Die Wahrscheinlichkeit, eine Königin zu ziehen, beträgt \(\frac{4}{52} = \frac{1}{13}\)
2) Wie groß ist die Wahrscheinlichkeit, beim Würfeln eine gerade Augenzahl zu erhalten?
Lösung: Gesamtzahl der Ergebnisse = 6
Gesamtzahl der positiven Ergebnisse = 3 (gerade Zahlen sind 2, 4 und 6)
Daher beträgt die Wahrscheinlichkeit, eine gerade Zahl zu erhalten \(\frac{3}{6} = \frac{1}{2}\)