probability

If today is Sunday than tomorrow being Monday is certain. The sun will certainly rise in the east. Also, it is impossible that you would grow taller than a giraffe. For a few events, we are certain of the outcome. But think of the situation where you are competing with eight other runners to win the race. You may win the race but it is not certain. When you buy a lottery ticket, you may win. But since lakhs of people have bought the tickets for the same lottery, the chances of you winning is very less.

The chances of happening of an event when measured quantitatively are called probability. Probability uses numbers to measure the chance of an outcome happening. Probability of an outcome can be shown using below scale:

 

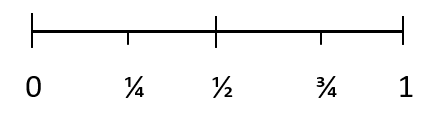
All probability have a value between 0 and 1. The probability of an impossible outcome is 0. And the probability of a certain outcome is 1. 1/4 represents an event unlikely to occur, 1/2 represents an even chance of occurrence of an event and 3/4 represents an event likely to occur.

Let's mark each of these outcomes on a probability scale:

• It is very likely to snow in Chicago in the month of December. (probability around 3/4)
• A coin has an even chance of landing on the head. (probability 1/2)
• It is impossible to be one year younger the following year(probability 0)
• It is definite that the sun will set in the west(probability 1)

The probability of the happening of an event E, denoted by P(E), is defined as

\(P(E) =\frac{\textrm{Number of favorable outcomes}}{\textrm{Total number of possible outcomes}} = \frac{e}{n}\)

where the outcome is a result of the experiment. A favourable outcome is that event the probability of whose occurrence we wish to determine.  

Let's learn the probability with a few examples:

1) If a card is drawn from a well-shuffled deck of 52 cards, what is the probability of drawing a queen? 

Solution: Total number of possible outcomes = 52

There are 4 queens in a deck of 52 cards and anyone queen can be drawn.

Therefore, the number of favourable outcomes = 4

The probability of drawing a queen is \(\frac{4}{52} = \frac{1}{13}\)

2) What is the probability of getting an even number when a dice is thrown?

Solution: Total number of outcomes = 6

Total number of favourable outcomes = 3 (even numbers are 2, 4 and 6)

Therefore, the probability to get an even number is \(\frac{3}{6} = \frac{1}{2}\)