Si hoy es domingo, es seguro que mañana será lunes. Seguramente el sol saldrá por el este. Además, es imposible que crezcas más que una jirafa. En algunos casos, estamos seguros del resultado. Pero piensa en la situación en la que estás compitiendo con otros ocho corredores para ganar la carrera. Puedes ganar la carrera, pero no es seguro. Cuando compras un billete de lotería, puedes ganar. Pero como miles de personas han comprado boletos para la misma lotería, las posibilidades de ganar son muy menores.
Las posibilidades de que ocurra un evento cuando se miden cuantitativamente se llaman probabilidad. La probabilidad usa números para medir la probabilidad de que ocurra un resultado. La probabilidad de un resultado se puede mostrar utilizando la siguiente escala:
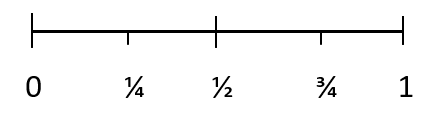
Toda probabilidad tiene un valor entre 0 y 1. La probabilidad de un resultado imposible es 0. Y la probabilidad de un resultado determinado es 1. 1/4 representa un evento que es poco probable que ocurra, 1/2 representa una posibilidad uniforme de que ocurra un evento y 3/4 representa un evento que probablemente ocurra.
Marquemos cada uno de estos resultados en una escala de probabilidad:
La probabilidad de que ocurra un evento E, denotada por P(E), se define como
\(P(E) =\frac{\textrm{Número de resultados favorables}}{\textrm{Número total de resultados posibles}} = \frac{e}{n}\)
donde el resultado es el resultado del experimento. Un resultado favorable es aquel evento cuya probabilidad de ocurrencia deseamos determinar.
Aprendamos la probabilidad con algunos ejemplos:
1) Si se saca una carta de una baraja de 52 cartas bien barajada, ¿cuál es la probabilidad de sacar una reina?
Solución: Número total de resultados posibles = 52
Hay 4 reinas en una baraja de 52 cartas y se puede sacar cualquier reina.
Por lo tanto, el número de resultados favorables = 4
La probabilidad de sacar una reina es \(\frac{4}{52} = \frac{1}{13}\)
2) ¿Cuál es la probabilidad de obtener un número par al lanzar un dado?
Solución: Número total de resultados = 6
Número total de resultados favorables = 3 (los números pares son 2, 4 y 6)
Por lo tanto, la probabilidad de obtener un número par es \(\frac{3}{6} = \frac{1}{2}\)