Si aujourd’hui c’est dimanche, demain sera lundi, c’est certain. Le soleil se lèvera certainement à l'est. De plus, il est impossible que vous deveniez plus grand qu’une girafe. Pour quelques événements, nous sommes certains du résultat. Mais pensez à la situation où vous êtes en compétition avec huit autres coureurs pour remporter la course. Vous pouvez gagner la course mais ce n'est pas certain. Lorsque vous achetez un billet de loterie, vous pouvez gagner. Mais comme des milliers de personnes ont acheté des billets pour la même loterie, les chances de gagner sont très moindres.
Les chances qu'un événement se produise lorsqu'elles sont mesurées quantitativement sont appelées probabilité. La probabilité utilise des nombres pour mesurer la probabilité qu'un résultat se produise. La probabilité d'un résultat peut être affichée à l'aide de l'échelle ci-dessous :
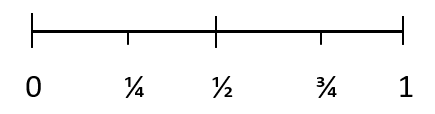
Toutes les probabilités ont une valeur comprise entre 0 et 1. La probabilité d'un résultat impossible est de 0. Et la probabilité d'un certain résultat est de 1. 1/4 représente un événement peu susceptible de se produire, 1/2 représente une chance égale d'occurrence d'un événement. événement et 3/4 représente un événement susceptible de se produire.
Marquons chacun de ces résultats sur une échelle de probabilité :
La probabilité qu'un événement E se produise, notée P(E), est définie comme
\(P(E) =\frac{\textrm{Nombre d'issues favorables}}{\textrm{Nombre total de résultats possibles}} = \frac{e}{n}\)
où le résultat est le résultat de l’expérience. Un résultat favorable est cet événement dont nous souhaitons déterminer la probabilité de survenance.
Apprenons la probabilité avec quelques exemples :
1) Si une carte est tirée d’un jeu de 52 cartes bien mélangé, quelle est la probabilité de tirer une reine ?
Solution : Nombre total de résultats possibles = 52
Il y a 4 reines dans un jeu de 52 cartes et n'importe quelle reine peut être tirée.
Donc le nombre d’issues favorables = 4
La probabilité de tirer une reine est \(\frac{4}{52} = \frac{1}{13}\)
2) Quelle est la probabilité d’obtenir un nombre pair lorsqu’un dé est lancé ?
Solution : Nombre total de résultats = 6
Nombre total de résultats favorables = 3 (les nombres pairs sont 2, 4 et 6)
Par conséquent, la probabilité d’obtenir un nombre pair est \(\frac{3}{6} = \frac{1}{2}\)