यदि आज रविवार है तो कल सोमवार होना निश्चित है। सूर्य निश्चित ही पूर्व दिशा से उगेगा। इसके अलावा, यह भी असंभव है कि आप जिराफ से लंबे हो जाएं। कुछ घटनाओं के लिए, हम परिणाम के बारे में निश्चित हैं। लेकिन उस स्थिति के बारे में सोचें जहां आप दौड़ जीतने के लिए आठ अन्य धावकों के साथ प्रतिस्पर्धा कर रहे हैं। आप रेस जीत सकते हैं लेकिन यह निश्चित नहीं है। जब आप लॉटरी टिकट खरीदते हैं, तो आप जीत सकते हैं। लेकिन चूंकि एक ही लॉटरी के लिए लाखों लोगों ने टिकट खरीदे हैं, इसलिए आपके जीतने की संभावना बहुत कम है।
किसी घटना को मात्रात्मक रूप से मापने पर उसके घटित होने की संभावना को संभाव्यता कहा जाता है। किसी परिणाम के घटित होने की संभावना को मापने के लिए संभाव्यता संख्याओं का उपयोग करती है। किसी परिणाम की संभावना को नीचे दिए गए पैमाने का उपयोग करके दिखाया जा सकता है:
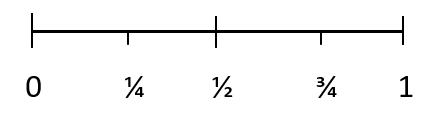
सभी संभावनाओं का मान 0 और 1 के बीच होता है। असंभव परिणाम की संभावना 0 है। और एक निश्चित परिणाम की संभावना 1 है। 1/4 एक ऐसी घटना को दर्शाता है जिसके घटित होने की संभावना नहीं है, 1/2 किसी घटना के घटित होने की सम संभावना को दर्शाता है। घटना और 3/4 घटित होने वाली संभावित घटना का प्रतिनिधित्व करता है।
आइए इनमें से प्रत्येक परिणाम को संभाव्यता पैमाने पर चिह्नित करें:
किसी घटना E के घटित होने की प्रायिकता को P(E) द्वारा निरूपित किया जाता है
\(P(E) =\frac{\textrm{अनुकूल परिणामों की संख्या}}{\textrm{संभावित परिणामों की कुल संख्या}} = \frac{e}{n}\)
जहां परिणाम प्रयोग का परिणाम है। अनुकूल परिणाम वह घटना है जिसके घटित होने की प्रायिकता हम निर्धारित करना चाहते हैं।
आइए कुछ उदाहरणों से संभाव्यता सीखें:
1) यदि 52 ताशों की अच्छी तरह से फेंटी गई गड्डी से एक पत्ता निकाला जाता है, तो रानी निकलने की प्रायिकता क्या है?
समाधान: संभावित परिणामों की कुल संख्या = 52
52 पत्तों की एक गड्डी में 4 रानियाँ हैं और किसी भी रानी को निकाला जा सकता है।
अत: अनुकूल परिणामों की संख्या = 4
एक रानी निकालने की प्रायिकता \(\frac{4}{52} = \frac{1}{13}\) है
2) पासा फेंकने पर सम संख्या प्राप्त होने की प्रायिकता क्या है?
समाधान: परिणामों की कुल संख्या = 6
अनुकूल परिणामों की कुल संख्या = 3 (सम संख्याएँ 2, 4 और 6 हैं)
इसलिए, एक सम संख्या प्राप्त होने की प्रायिकता \(\frac{3}{6} = \frac{1}{2}\) है