Ako je danas nedjelja, sigurno je da će sutra biti ponedjeljak. Sunce će sigurno izaći na istoku. Također, nemoguće je da biste narasli viši od žirafe. Za nekoliko smo događaja sigurni u ishod. Ali razmislite o situaciji u kojoj se natječete s osam drugih trkača za pobjedu u utrci. Možete pobijediti u utrci, ali nije sigurno. Kad kupite srećku, možete dobiti. Ali budući da je milijune ljudi kupilo listiće za istu lutriju, šanse da dobijete vrlo su manje.
Kvantitativno mjerene šanse da se dogodi neki događaj nazivaju se vjerojatnost. Vjerojatnost koristi brojeve za mjerenje šanse da se ishod dogodi. Vjerojatnost ishoda može se prikazati korištenjem donje ljestvice:
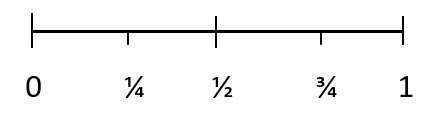
Sve vjerojatnosti imaju vrijednost između 0 i 1. Vjerojatnost nemogućeg ishoda je 0. A vjerojatnost određenog ishoda je 1. 1/4 predstavlja događaj za koji je malo vjerojatno da će se dogoditi, 1/2 predstavlja jednaku šansu da se dogodi događaj, a 3/4 predstavlja događaj koji će se vjerojatno dogoditi.
Označimo svaki od ovih ishoda na skali vjerojatnosti:
Vjerojatnost događanja događaja E, označena s P(E), definirana je kao
\(P(E) =\frac{\textrm{Broj povoljnih ishoda}}{\textrm{Ukupan broj mogućih ishoda}} = \frac{e}{n}\)
gdje je rezultat rezultat eksperimenta. Povoljan ishod je onaj događaj čiju vjerojatnost nastanka želimo utvrditi.
Naučimo vjerojatnost na nekoliko primjera:
1) Ako je karta izvučena iz dobro promiješanog špila od 52 karte, kolika je vjerojatnost izvlačenja dame?
Rješenje: Ukupan broj mogućih ishoda = 52
Postoje 4 dame u špilu od 52 karte i može se izvući bilo koja dama.
Dakle, broj povoljnih ishoda = 4
Vjerojatnost izvlačenja dame je \(\frac{4}{52} = \frac{1}{13}\)
2) Kolika je vjerojatnost da dobijete paran broj kada se kocka baci?
Rješenje: Ukupan broj ishoda = 6
Ukupan broj povoljnih ishoda = 3 (parni brojevi su 2, 4 i 6)
Stoga je vjerojatnost da se dobije paran broj \(\frac{3}{6} = \frac{1}{2}\)