今日が日曜日であれば、明日が月曜日であることは確実です。太陽は必ず東から昇ります。また、キリンよりも身長が伸びることは不可能です。いくつかのイベントについては、結果が確実にわかっています。しかし、レースに勝つために他の 8 人のランナーと競争している状況を考えてみましょう。あなたはレースに勝つかもしれませんが、それは確実ではありません。宝くじを買うと当たるかもしれません。しかし、何十万人もの人が同じ宝くじのチケットを購入しているため、当たる可能性は非常に低くなります。
定量的に測定した場合の事象が起こる確率を確率といいます。確率では、結果が起こる確率を数値を使用して測定します。結果の確率は、以下のスケールを使用して表示できます。
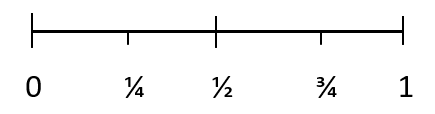
すべての確率は 0 と 1 の間の値を持ちます。不可能な結果の確率は 0 です。そして、特定の結果の確率は 1 です。1/4 はイベントが発生する可能性が低いことを表し、1/2 はイベントが発生する偶数の確率を表します。イベント、3/4 は発生する可能性のあるイベントを表します。
これらの結果をそれぞれ確率スケールでマークしてみましょう。
イベント E が発生する確率は P(E) で表され、次のように定義されます。
\(P(E) =\frac{\textrm{良好な結果の数}}{\textrm{起こり得る結果の総数}} = \frac{e}{n}\)
ここで、結果は実験の結果です。好ましい結果とは、その発生確率を決定したいイベントです。
いくつかの例で確率を学びましょう。
1) 52 枚のカードをよくシャッフルしたデッキからカードを引いた場合、クイーンを引く確率はいくらですか?
解決策: 考えられる結果の総数 = 52
52 枚のカードのデッキには 4 人のクイーンがあり、誰でもクイーンを引くことができます。
したがって、好ましい結果の数 = 4
クイーンを引く確率は\(\frac{4}{52} = \frac{1}{13}\)です
2) サイコロを振ったときに偶数が出る確率はどれくらいですか?
解決策: 結果の総数 = 6
好ましい結果の合計数 = 3 (偶数は 2、4、6)
したがって、偶数を取得する確率は\(\frac{3}{6} = \frac{1}{2}\)となります。