Ако денес е недела, утре е сигурно понеделник. Сонцето сигурно ќе изгрее на исток. Исто така, невозможно е да пораснете повисок од жирафа. За неколку настани, сигурни сме во исходот. Но, размислете за ситуацијата кога се натпреварувате со осум други тркачи за да победите на трката. Можеби ќе победите во трката, но тоа не е сигурно. Кога ќе купите лотарија, може да добиете. Но, бидејќи милиони луѓе купиле билети за истата лотарија, шансите да победите се многу помали.
Шансите да се случи некој настан кога се мери квантитативно се нарекуваат веројатност. Веројатноста користи бројки за да ја измери шансата да се случи исход. Веројатноста за исход може да се прикаже со помош на следната скала:
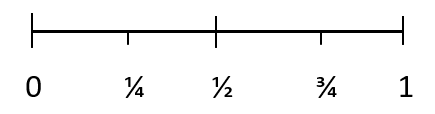
Сите веројатности имаат вредност помеѓу 0 и 1. Веројатноста за невозможен исход е 0. А веројатноста за одреден исход е 1. 1/4 претставува настан што нема веројатност да се случи, 1/2 претставува рамномерна шанса за појава на настан и 3/4 претставува настан кој најверојатно ќе се случи.
Ајде да го означиме секој од овие резултати на скала на веројатност:
Веројатноста да се случи настан E, означен со P(E), се дефинира како
\(P(E) =\frac{\textrm{Број на поволни исходи}}{\textrm{Вкупен број на можни исходи}} = \frac{e}{n}\)
каде што исходот е резултат на експериментот. Поволен исход е тој настан чија веројатност сакаме да ја одредиме.
Ајде да ја научиме веројатноста со неколку примери:
1) Ако картата е извлечена од добро измешана палуба од 52 карти, колкава е веројатноста да се извлече кралица?
Решение: Вкупен број на можни исходи = 52
Има 4 кралици во шпил од 52 карти и секоја кралица може да биде извлечена.
Според тоа, бројот на поволни исходи = 4
Веројатноста да се нацрта кралица е \(\frac{4}{52} = \frac{1}{13}\)
2) Која е веројатноста да се добие парен број кога ќе се фрли коцка?
Решение: Вкупен број на исходи = 6
Вкупен број на поволни исходи = 3 (парни броеви се 2, 4 и 6)
Затоа, веројатноста да се добие парен број е \(\frac{3}{6} = \frac{1}{2}\)