Хэрэв өнөөдөр ням гараг бол маргааш даваа гараг байх нь гарцаагүй. Нар зүүн талаараа мандах нь гарцаагүй. Мөн та анаашаас өндөр болно гэдэг боломжгүй юм. Хэд хэдэн үйл явдлын хувьд бид үр дүнд нь итгэлтэй байна. Гэхдээ та бусад найман гүйгчтэй уралдаж түрүүлэхийн тулд ямар нөхцөл байдалд байгааг бодоорой. Та уралдаанд түрүүлж магадгүй ч энэ нь тодорхойгүй байна. Та сугалааны тасалбар худалдаж авбал хожих боломжтой. Гэхдээ нэг сугалааны тасалбарыг олон сая хүн худалдаж авсан тул хожих магадлал маш бага байна.
Үйл явдал болох магадлалыг тоон үзүүлэлтээр хэмжсэн тохиолдолд магадлал гэнэ. Магадлал нь үр дүн гарах магадлалыг хэмжихэд тоо ашигладаг. Үр дүнгийн магадлалыг дараах хуваарийг ашиглан харуулж болно.
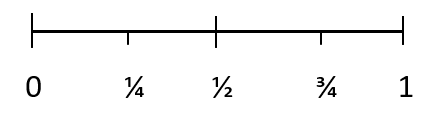
Бүх магадлал нь 0-ээс 1-ийн хооронд утгатай байна. Боломжгүй үр дүнгийн магадлал нь 0. Мөн тодорхой үр дүнгийн магадлал 1. 1/4 нь тохиолдох магадлал багатай үйл явдлыг, 1/2 нь тохиолдох магадлалыг илэрхийлдэг. үйл явдал ба 3/4 нь тохиолдох магадлалтай үйл явдлыг илэрхийлнэ.
Эдгээр үр дүн бүрийг магадлалын хэмжүүрээр тэмдэглэе:
P(E)-ээр тэмдэглэсэн E үйл явдлын тохиолдох магадлалыг дараах байдлаар тодорхойлно
\(P(E) =\frac{\textrm{Тааламжтай үр дүнгийн тоо}}{\textrm{Боломжит үр дүнгийн нийт тоо}} = \frac{e}{n}\)
үр дүн нь туршилтын үр дүн юм. Тааламжтай үр дүн нь тухайн үйл явдал хэний тохиолдох магадлалыг тодорхойлохыг хүсч байна.
Хэд хэдэн жишээгээр магадлалыг сурцгаая:
1) Хэрэв 52 хөзрийг сайтар хольсон тавцангаас карт зурсан бол хатан хаан зурах магадлал хэд вэ?
Шийдэл: Боломжит үр дүнгийн нийт тоо = 52
52 хөзрийн тавцанд 4 хатан байх ба бүх хатан хааныг зурж болно.
Тиймээс таатай үр дүнгийн тоо = 4
Хатан зурах магадлал нь \(\frac{4}{52} = \frac{1}{13}\)
2) Шоо шидэхэд тэгш тоо гарах магадлал хэд вэ?
Шийдэл: Нийт үр дүнгийн тоо = 6
Тааламжтай үр дүнгийн нийт тоо = 3 (тэгш тоо нь 2, 4, 6)
Тиймээс тэгш тоо гарах магадлал нь \(\frac{3}{6} = \frac{1}{2}\)