ဒီနေ့ တနင်္ဂနွေဆိုရင် မနက်ဖြန် တနင်္လာထက် သေချာပါတယ်။ အရှေ့ဘက်တွင် နေထွက်မည်မှာ သေချာသည်။ ထို့အပြင် သင်သည် သစ်ကုလားအုတ်ထက် အရပ်ရှည်ရန် မဖြစ်နိုင်ပေ။ အချို့သော အဖြစ်အပျက်များအတွက် ကျွန်ုပ်တို့သည် ရလဒ်ကို သေချာပါသည်။ ဒါပေမယ့် ပြိုင်ပွဲမှာ အနိုင်ရဖို့ တခြားအပြေးသမား ရှစ်ယောက်နဲ့ ယှဉ်ပြိုင်ရမယ့် အခြေအနေကို စဉ်းစားကြည့်ပါ။ ပြိုင်ပွဲမှာ သင်အနိုင်ရနိုင်ပေမယ့် မသေချာပါဘူး။ ထီထိုးတဲ့အခါ အောင်နိုင်မယ်။ ဒါပေမယ့် ထီတူတူလက်မှတ်တွေကို လူပေါင်းသိန်းနဲ့ချီပြီးဝယ်ထားတာကြောင့် သင်အနိုင်ရဖို့အခွင့်အရေးက အရမ်းနည်းပါတယ်။
အရေအတွက်အားဖြင့် တိုင်းတာသောအခါ အဖြစ်အပျက်တစ်ခု ဖြစ်ပွားနိုင်ခြေကို ဖြစ်နိုင်ခြေဟု ခေါ်သည်။ Probability သည် ရလဒ်ဖြစ်ပေါ်နိုင်ခြေကို တိုင်းတာရန် နံပါတ်များကို အသုံးပြုသည်။ အောက်ပါစကေးကို အသုံးပြု၍ ရလဒ်တစ်ခု၏ ဖြစ်နိုင်ခြေကို ပြနိုင်သည်-
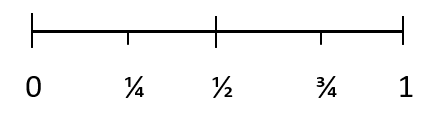
ဖြစ်နိုင်ခြေအားလုံးသည် 0 နှင့် 1 အကြားတန်ဖိုးရှိသည်။ မဖြစ်နိုင်သောရလဒ်တစ်ခု၏ဖြစ်နိုင်ခြေမှာ 0 ဖြစ်သည်။ နှင့် အချို့သောရလဒ်များ၏ဖြစ်နိုင်ခြေမှာ 1 ဖြစ်သည်။ 1/4 သည် ဖြစ်ပေါ်လာရန်မဖြစ်နိုင်သောဖြစ်ရပ်ကိုကိုယ်စားပြုသည်၊ 1/2 သည် တူညီသောရလဒ်တစ်ခုဖြစ်လာနိုင်ချေကိုကိုယ်စားပြုသည်။ ဖြစ်ရပ်နှင့် 3/4 သည် ဖြစ်ပေါ်လာမည့် အဖြစ်အပျက်ကို ကိုယ်စားပြုသည်။
ဖြစ်နိုင်ခြေအတိုင်းအတာတစ်ခုစီတွင် ဤရလဒ်များကို အမှတ်အသားပြုကြပါစို့။
P(E) ဖြင့်ဖော်ပြသော ဖြစ်ရပ် E ၏ဖြစ်နိုင်ခြေကို သတ်မှတ်သည်။
\(P(E) =\frac{\textrm{ကောင်းသောရလဒ်များအရေအတွက်}}{\textrm{ဖြစ်နိုင်ခြေရှိသော ရလဒ်စုစုပေါင်း}} = \frac{e}{n}\)
ရလဒ်သည် စမ်းသပ်မှု၏ရလဒ်ဖြစ်သည်။ အခွင့်သာသော ရလဒ်တစ်ခုသည် ကျွန်ုပ်တို့ ဆုံးဖြတ်လိုသော ဖြစ်ပျက်မှု၏ ဖြစ်နိုင်ခြေကို ထိုအဖြစ်အပျက်ဖြစ်သည်။
ဥပမာအနည်းငယ်ဖြင့် ဖြစ်နိုင်ခြေကို လေ့လာကြပါစို့။
1) ကတ်တစ်ကတ်ကို 52 ကတ်ပါ ကောင်းမွန်စွာ ပေါင်းစပ်ထားသော ကုန်းပတ်မှ ထုတ်ယူပါက၊ ဘုရင်မတစ်ဦးကို ဆွဲနိုင်ခြေ မည်မျှရှိသနည်း။
ဖြေရှင်းချက်- ဖြစ်နိုင်ခြေရှိသော ရလဒ်စုစုပေါင်း = 52
ကဒ် 52 ခုပါသောကုန်းပတ်တွင်ဘုရင်မ 4 ခုရှိပြီးမည်သူမဆိုဘုရင်မကိုဆွဲနိုင်သည်။
ထို့ကြောင့် အခွင့်သာသော ရလဒ်အရေအတွက် = ၄
ဘုရင်မပုံဆွဲရန် ဖြစ်နိုင်ခြေမှာ \(\frac{4}{52} = \frac{1}{13}\)
2) အန်စာတုံးတစ်ခုချလိုက်တဲ့အခါ ဂဏန်းတစ်လုံးရဖို့ ဖြစ်နိုင်ခြေဘယ်လောက်ရှိလဲ။
ဖြေရှင်းချက်- စုစုပေါင်းရလဒ်များ = 6
ကောင်းသောရလဒ်များ စုစုပေါင်းအရေအတွက် = 3 (ကိန်းဂဏန်းများသည် 2၊ 4 နှင့် 6)
ထို့ကြောင့်၊ ကိန်းဂဏန်းတစ်ခုရရန် ဖြစ်နိုင်ခြေမှာ \(\frac{3}{6} = \frac{1}{2}\)