आज आइतबार भन्दा भोलि सोमबार हुने निश्चित छ। पूर्वमा सूर्य अवश्य उदाउनेछ। साथै, यो असम्भव छ कि तपाईं जिराफ भन्दा अग्लो हुनुहुनेछ। केही घटनाहरूको लागि, हामी नतिजामा निश्चित छौं। तर दौड जित्नको लागि तपाईले अन्य आठ धावकहरूसँग प्रतिस्पर्धा गर्दै हुनुहुन्छ भन्ने अवस्थाको बारेमा सोच्नुहोस्। तपाइँ दौड जित्न सक्नुहुन्छ तर यो निश्चित छैन। जब तपाइँ लटरी टिकट खरिद गर्नुहुन्छ, तपाइँ जित्न सक्नुहुन्छ। तर लाखौं मानिसहरूले एउटै लटरीको लागि टिकटहरू किनेका हुनाले, तपाईंको जित्ने सम्भावना धेरै कम छ।
परिमाणात्मक मापन गर्दा घटना घट्ने सम्भावनालाई सम्भाव्यता भनिन्छ। सम्भाव्यताले परिणाम हुने सम्भावना मापन गर्न संख्याहरू प्रयोग गर्दछ। नतिजाको सम्भाव्यता तलको स्केल प्रयोग गरेर देखाउन सकिन्छ:
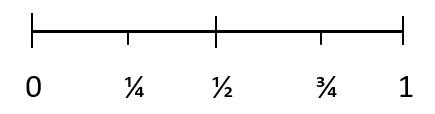
सबै सम्भाव्यताको मान ० र १ को बीचमा हुन्छ। असम्भव नतिजाको सम्भाव्यता ० हो। र निश्चित परिणामको सम्भाव्यता १ हो। १/४ ले घट्न नसकिने घटनालाई प्रतिनिधित्व गर्दछ, १/२ ले घटना हुने सम्भावनालाई प्रतिनिधित्व गर्दछ। घटना र 3/4 ले सम्भावित घटनालाई प्रतिनिधित्व गर्दछ।
यी प्रत्येक परिणामहरूलाई सम्भाव्यता मापनमा चिन्ह लगाउनुहोस्:
घटना E को घटना को सम्भाव्यता, P(E) द्वारा निहित, को रूपमा परिभाषित गरिएको छ
\(P(E) =\frac{\textrm{अनुकूल परिणामहरूको संख्या}}{\textrm{सम्भावित परिणामहरूको कुल संख्या}} = \frac{e}{n}\)
जहाँ परिणाम प्रयोगको परिणाम हो। एउटा अनुकूल परिणाम त्यो घटना हो जसको घटनाको सम्भावना हामी निर्धारण गर्न चाहन्छौं।
केहि उदाहरणहरु संग सम्भाव्यता जानौं:
1) यदि 52 कार्डहरूको राम्रोसँग मिलाइएको डेकबाट कार्ड कोरिएको छ भने, रानी कोर्ने सम्भावना के हो?
समाधान: सम्भावित परिणामहरूको कुल संख्या = 52
52 कार्डको डेकमा 4 रानीहरू छन् र कुनै पनि रानी कोर्न सकिन्छ।
त्यसकारण, अनुकूल परिणामहरूको संख्या = 4
रानी कोर्ने सम्भावना \(\frac{4}{52} = \frac{1}{13}\)
2) पासा फ्याँक्दा सम संख्या प्राप्त हुने सम्भावना के हो?
समाधान: परिणामहरूको कुल संख्या = 6
अनुकूल परिणामहरूको कुल संख्या = 3 (सही संख्याहरू 2, 4 र 6 हुन्)
त्यसकारण, सम संख्या प्राप्त गर्ने सम्भावना \(\frac{3}{6} = \frac{1}{2}\)