Als het vandaag zondag is, dan is het morgen zeker maandag. De zon zal zeker in het oosten opkomen. Bovendien is het onmogelijk dat je groter wordt dan een giraffe. Voor een aantal evenementen zijn we zeker van de uitkomst. Maar denk eens aan de situatie waarin je met acht andere lopers strijdt om de race te winnen. Je kunt de race winnen, maar dat is niet zeker. Als u een lot uit de loterij koopt, kunt u winnen. Maar aangezien heel veel mensen kaartjes voor dezelfde loterij hebben gekocht, is de kans dat je wint veel kleiner.
De kans dat een gebeurtenis plaatsvindt, kwantitatief gemeten, wordt waarschijnlijkheid genoemd. Waarschijnlijkheid gebruikt getallen om de kans op een uitkomst te meten. De waarschijnlijkheid van een uitkomst kan worden weergegeven met behulp van de onderstaande schaal:
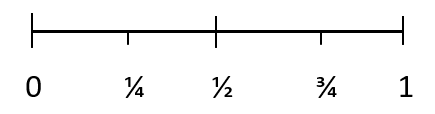
Alle waarschijnlijkheden hebben een waarde tussen 0 en 1. De waarschijnlijkheid van een onmogelijke uitkomst is 0. En de waarschijnlijkheid van een bepaalde uitkomst is 1. 1/4 vertegenwoordigt een gebeurtenis die waarschijnlijk niet zal plaatsvinden, 1/2 vertegenwoordigt een gelijke kans op het optreden van een gebeurtenis. gebeurtenis en 3/4 vertegenwoordigt een gebeurtenis die waarschijnlijk zal plaatsvinden.
Laten we elk van deze uitkomsten op een waarschijnlijkheidsschaal markeren:
De waarschijnlijkheid dat een gebeurtenis E plaatsvindt, aangegeven met P(E), wordt gedefinieerd als:
\(P(E) =\frac{\textrm{Aantal gunstige uitkomsten}}{\textrm{Totaal aantal mogelijke uitkomsten}} = \frac{e}{n}\)
waarbij de uitkomst het resultaat is van het experiment. Een gunstige uitkomst is die gebeurtenis waarvan we de waarschijnlijkheid willen bepalen.
Laten we de waarschijnlijkheid leren met een paar voorbeelden:
1) Als een kaart wordt getrokken uit een goed geschud spel van 52 kaarten, wat is dan de kans dat er een koningin wordt getrokken?
Oplossing: Totaal aantal mogelijke uitkomsten = 52
Er zijn 4 koninginnen in een kaartspel van 52 kaarten en elke koningin kan getrokken worden.
Daarom is het aantal gunstige uitkomsten = 4
De kans op het trekken van een koningin is \(\frac{4}{52} = \frac{1}{13}\)
2) Wat is de kans op een even getal als er met een dobbelsteen wordt gegooid?
Oplossing: Totaal aantal uitkomsten = 6
Totaal aantal gunstige uitkomsten = 3 (even getallen zijn 2, 4 en 6)
Daarom is de kans op een even getal \(\frac{3}{6} = \frac{1}{2}\)