Jeśli dzisiaj jest niedziela, to pewne jest, że jutro będzie poniedziałek. Słońce z pewnością wzejdzie na wschodzie. Poza tym niemożliwe jest, abyś urósł wyższy od żyrafy. W przypadku kilku wydarzeń jesteśmy pewni wyniku. Ale pomyśl o sytuacji, w której rywalizujesz z ośmioma innymi biegaczami o zwycięstwo w wyścigu. Być może wygrasz wyścig, ale nie jest to pewne. Kupując los na loterię, możesz wygrać. Ale ponieważ miliony ludzi kupiło losy na tę samą loterię, szanse na wygraną są bardzo mniejsze.
Szanse wystąpienia zdarzenia mierzone ilościowo nazywane są prawdopodobieństwem. Prawdopodobieństwo wykorzystuje liczby do pomiaru szansy na wystąpienie wyniku. Prawdopodobieństwo wyniku można przedstawić za pomocą poniższej skali:
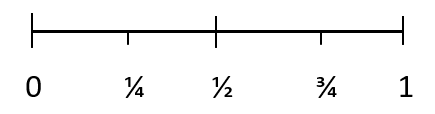
Każde prawdopodobieństwo ma wartość pomiędzy 0 a 1. Prawdopodobieństwo niemożliwego wyniku wynosi 0. A prawdopodobieństwo określonego wyniku wynosi 1. 1/4 reprezentuje zdarzenie mało prawdopodobne, 1/2 oznacza parzystą szansę wystąpienia zdarzenie, a 3/4 oznacza zdarzenie, które może wystąpić.
Oznaczmy każdy z tych wyników na skali prawdopodobieństwa:
Prawdopodobieństwo zajścia zdarzenia E, oznaczone jako P(E), definiuje się jako
\(P(E) =\frac{\textrm{Liczba korzystnych wyników}}{\textrm{Całkowita liczba możliwych wyników}} = \frac{e}{n}\)
gdzie wynik jest wynikiem eksperymentu. Wynik korzystny to zdarzenie, którego prawdopodobieństwo wystąpienia chcemy określić.
Nauczmy się prawdopodobieństwa na kilku przykładach:
1) Jeśli zostanie wyciągnięta karta z dobrze potasowanej talii 52 kart, jakie jest prawdopodobieństwo wylosowania królowej?
Rozwiązanie: Całkowita liczba możliwych wyników = 52
W talii 52 kart znajdują się 4 królowe i można wylosować dowolną królową.
Zatem liczba korzystnych wyników = 4
Prawdopodobieństwo wylosowania królowej wynosi \(\frac{4}{52} = \frac{1}{13}\)
2) Jakie jest prawdopodobieństwo, że w rzucie kostką wypadnie liczba parzysta?
Rozwiązanie: Całkowita liczba wyników = 6
Całkowita liczba korzystnych wyników = 3 (liczby parzyste to 2, 4 i 6)
Dlatego prawdopodobieństwo otrzymania liczby parzystej wynosi \(\frac{3}{6} = \frac{1}{2}\)