Если сегодня воскресенье, то завтра понедельник наверняка. Солнце обязательно взойдет на востоке. Кроме того, невозможно, чтобы вы выросли выше жирафа. В отношении некоторых событий мы уверены в исходе. Но подумайте о ситуации, когда вы соревнуетесь с восемью другими бегунами за победу в забеге. Вы можете выиграть гонку, но это не обязательно. Купив лотерейный билет, вы можете выиграть. Но поскольку билеты одной и той же лотереи купили тысячи людей, шансы на ваш выигрыш очень малы.
Вероятность наступления события, измеренная количественно, называется вероятностью. Вероятность использует числа для измерения вероятности наступления результата. Вероятность исхода можно показать, используя приведенную ниже шкалу:
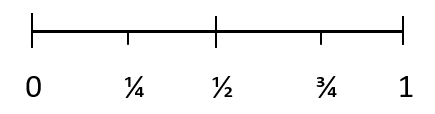
Все вероятности имеют значение от 0 до 1. Вероятность невозможного результата равна 0. А вероятность определенного результата равна 1. 1/4 представляет событие, которое маловероятно произойдет, 1/2 представляет собой четную вероятность возникновения события. событие, а 3/4 представляет событие, которое может произойти.
Давайте отметим каждый из этих исходов по шкале вероятности:
Вероятность наступления события E, обозначаемая P(E), определяется как
\(P(E) =\frac{\textrm{Количество благоприятных исходов}}{\textrm{Общее количество возможных исходов}} = \frac{e}{n}\)
где результат является результатом эксперимента. Благоприятный исход – это событие, вероятность наступления которого мы хотим определить.
Давайте изучим вероятность на нескольких примерах:
1) Если из хорошо перетасованной колоды, состоящей из 52 карт, вытянута карта, какова вероятность вытянуть даму?
Решение: Общее количество возможных исходов = 52.
В колоде из 52 карт 4 дамы, и можно взять любую даму.
Следовательно, количество благоприятных исходов = 4
Вероятность вытянуть ферзя равна \(\frac{4}{52} = \frac{1}{13}\)
2) Какова вероятность того, что при броске игральной кости выпадет четное число?
Решение: Общее количество исходов = 6.
Общее количество благоприятных исходов = 3 (четные числа — 2, 4 и 6)
Следовательно, вероятность получить четное число равна \(\frac{3}{6} = \frac{1}{2}\)