Om idag är söndag än imorgon är det säkert att vara måndag. Solen kommer säkert att gå upp i öster. Dessutom är det omöjligt att du skulle växa längre än en giraff. För några evenemang är vi säkra på resultatet. Men tänk på situationen där du tävlar med åtta andra löpare om att vinna loppet. Du kanske vinner loppet men det är inte säkert. När du köper en lott kan du vinna. Men eftersom tusentals människor har köpt lotterna till samma lotteri, är chansen att du vinner mycket mindre.
Chansen att inträffa av en händelse när den mäts kvantitativt kallas sannolikhet. Sannolikhet använder siffror för att mäta chansen att ett resultat inträffar. Sannolikheten för ett utfall kan visas med hjälp av nedanstående skala:
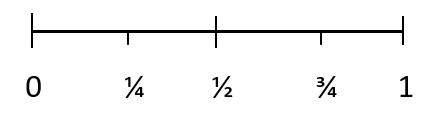
All sannolikhet har ett värde mellan 0 och 1. Sannolikheten för ett omöjligt utfall är 0. Och sannolikheten för ett visst utfall är 1. 1/4 representerar en händelse som osannolikt kommer att inträffa, 1/2 representerar en jämn chans att inträffa händelse och 3/4 representerar en händelse som sannolikt kommer att inträffa.
Låt oss markera vart och ett av dessa resultat på en sannolikhetsskala:
Sannolikheten för att en händelse E ska inträffa, betecknad med P(E), definieras som
\(P(E) =\frac{\textrm{Antal gynnsamma resultat}}{\textrm{Totalt antal möjliga utfall}} = \frac{e}{n}\)
där resultatet är ett resultat av experimentet. Ett gynnsamt resultat är den händelse vars sannolikhet vi vill bestämma.
Låt oss lära oss sannolikheten med några exempel:
1) Om ett kort dras från en väl blandad kortlek med 52 kort, vad är sannolikheten att dra en dam?
Lösning: Totalt antal möjliga utfall = 52
Det finns 4 damer i en kortlek med 52 kort och alla damer kan dras.
Därför är antalet gynnsamma resultat = 4
Sannolikheten att dra en dam är \(\frac{4}{52} = \frac{1}{13}\)
2) Vad är sannolikheten att få ett jämnt tal när en tärning kastas?
Lösning: Totalt antal utfall = 6
Totalt antal gynnsamma utfall = 3 (jämna tal är 2, 4 och 6)
Därför är sannolikheten att få ett jämnt tal \(\frac{3}{6} = \frac{1}{2}\)