Bugün Pazar ise yarının Pazartesi olacağı kesindir. Güneş mutlaka doğudan doğacak. Ayrıca zürafadan daha uzun olmanız da imkansızdır. Bazı olayların sonucundan eminiz. Ancak yarışı kazanmak için diğer sekiz koşucuyla rekabet ettiğiniz durumu düşünün. Yarışı kazanabilirsiniz ama bu kesin değil. Piyango bileti aldığınızda kazanabilirsiniz. Ancak binlerce insan aynı piyangonun biletlerini aldığından kazanma şansınız çok daha az.
Bir olayın niceliksel olarak ölçüldüğünde gerçekleşme şansına olasılık denir. Olasılık, bir sonucun gerçekleşme olasılığını ölçmek için sayıları kullanır. Bir sonucun olasılığı aşağıdaki ölçek kullanılarak gösterilebilir:
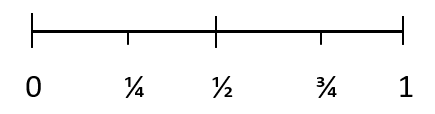
Tüm olasılıklar 0 ile 1 arasında bir değere sahiptir. İmkansız bir sonucun olasılığı 0'dır. Belirli bir sonucun olasılığı ise 1'dir. 1/4, gerçekleşmesi muhtemel olmayan bir olayı, 1/2 ise bir olayın meydana gelme olasılığını temsil eder. olayı, 3/4 ise gerçekleşmesi muhtemel bir olayı temsil eder.
Bu sonuçların her birini bir olasılık ölçeğinde işaretleyelim:
P(E) ile gösterilen E olayının gerçekleşme olasılığı şu şekilde tanımlanır:
\(P(E) =\frac{\textrm{Olumlu sonuçların sayısı}}{\textrm{Olası sonuçların toplam sayısı}} = \frac{e}{n}\)
sonucun deneyin bir sonucu olduğu yer. Olumlu sonuç, gerçekleşme olasılığını belirlemek istediğimiz olaydır.
Birkaç örnekle olasılığı öğrenelim:
1) İyi karıştırılmış 52 kartlık bir desteden bir kart çekilirse, vezir çekme olasılığı nedir?
Çözüm: Olası sonuçların toplam sayısı = 52
52 kartlık bir destede 4 kraliçe vardır ve herhangi bir kraliçe çekilebilir.
Bu nedenle, olumlu sonuçların sayısı = 4
Vezir çekme olasılığı \(\frac{4}{52} = \frac{1}{13}\) dir
2) Bir zar atıldığında çift sayı gelme olasılığı nedir?
Çözüm: Toplam sonuç sayısı = 6
Olumlu sonuçların toplam sayısı = 3 (çift sayılar 2, 4 ve 6'dır)
Bu nedenle çift sayı alma olasılığı \(\frac{3}{6} = \frac{1}{2}\) dir.