Якщо сьогодні неділя, то завтра точно буде понеділок. Сонце неодмінно зійде на сході. Крім того, неможливо, щоб ви виросли вище жирафа. Ми впевнені в результатах кількох подій. Але подумайте про ситуацію, коли ви змагаєтеся з вісьмома іншими бігунами, щоб виграти гонку. Ви можете виграти гонку, але це не напевно. Купуючи лотерейний квиток, ви можете виграти. Але оскільки тисячі людей купили квитки для однієї лотереї, шанси на ваш виграш значно менші.
Імовірність події, виміряна кількісно, називається ймовірністю. Імовірність використовує числа, щоб виміряти ймовірність досягнення результату. Імовірність результату можна показати за допомогою наступної шкали:
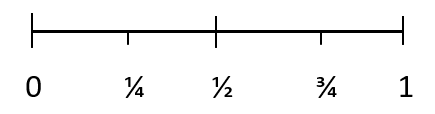
Усі ймовірності мають значення від 0 до 1. Імовірність неможливого результату дорівнює 0. А ймовірність певного результату дорівнює 1. 1/4 означає подію, яка малоймовірно відбудеться, 1/2 представляє рівну ймовірність появи подія, а 3/4 означає подію, яка ймовірно відбудеться.
Давайте позначимо кожен із цих результатів за шкалою ймовірності:
Імовірність настання події E, позначена P(E), визначається як
\(P(E) =\frac{\textrm{Кількість сприятливих результатів}}{\textrm{Загальна кількість можливих результатів}} = \frac{e}{n}\)
де результат є результатом експерименту. Сприятливий результат - це подія, ймовірність настання якої ми хочемо визначити.
Давайте дізнаємося ймовірність на кількох прикладах:
1) Яка ймовірність вилучення дами, якщо взяти карту з добре перемішаної колоди з 52 карт?
Рішення: Загальна кількість можливих результатів = 52
У колоді з 52 карт є 4 дами, і можна взяти будь-яку даму.
Отже, кількість сприятливих результатів = 4
Імовірність вилучення ферзя становить \(\frac{4}{52} = \frac{1}{13}\)
2) Яка ймовірність отримання парного числа під час кидання кубика?
Рішення: Загальна кількість результатів = 6
Загальна кількість сприятливих результатів = 3 (парні числа 2, 4 і 6)
Тому ймовірність отримати парне число дорівнює \(\frac{3}{6} = \frac{1}{2}\)