اگر آج اتوار ہے تو کل پیر ہونا یقینی ہے۔ سورج یقیناً مشرق میں نکلے گا۔ نیز، یہ ناممکن ہے کہ آپ زرافے سے لمبے ہو جائیں۔ چند واقعات کے لیے، ہم نتائج کے بارے میں یقین رکھتے ہیں۔ لیکن اس صورتحال کے بارے میں سوچیں جہاں آپ ریس جیتنے کے لیے آٹھ دوسرے رنرز کے ساتھ مقابلہ کر رہے ہیں۔ آپ ریس جیت سکتے ہیں لیکن یہ یقینی نہیں ہے۔ جب آپ لاٹری ٹکٹ خریدتے ہیں، تو آپ جیت سکتے ہیں۔ لیکن چونکہ لاکھوں لوگوں نے اسی لاٹری کے ٹکٹ خریدے ہیں، اس لیے آپ کے جیتنے کے امکانات بہت کم ہیں۔
کسی واقعہ کے ہونے کے امکانات کو جب مقداری طور پر ماپا جاتا ہے تو امکان کہلاتا ہے۔ امکان کسی نتیجے کے ہونے کے امکانات کی پیمائش کرنے کے لیے اعداد کا استعمال کرتا ہے۔ ذیل کے پیمانے کا استعمال کرتے ہوئے نتیجہ کا امکان دکھایا جا سکتا ہے:
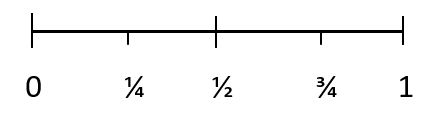
تمام احتمالات کی قدر 0 اور 1 کے درمیان ہوتی ہے۔ ایک ناممکن نتیجہ کا امکان 0 ہے۔ اور کسی خاص نتیجہ کا امکان 1 ہے۔ 1/4 ایک واقعہ کی نمائندگی کرتا ہے جس کا امکان نہیں ہے، 1/2 کسی کے وقوع پذیر ہونے کے برابر امکان کی نمائندگی کرتا ہے۔ واقعہ اور 3/4 پیش آنے والے واقعہ کی نمائندگی کرتا ہے۔
آئیے ان نتائج میں سے ہر ایک کو امکانی پیمانے پر نشان زد کریں:
P(E) کے ذریعہ اشارہ کردہ واقعہ E کے ہونے کا امکان اس طرح بیان کیا گیا ہے۔
\(P(E) =\frac{\textrm{سازگار نتائج کی تعداد}}{\textrm{ممکنہ نتائج کی کل تعداد}} = \frac{e}{n}\)
جہاں نتیجہ تجربہ کا نتیجہ ہے۔ ایک سازگار نتیجہ وہ واقعہ ہے جس کے وقوع پذیر ہونے کا ہم تعین کرنا چاہتے ہیں۔
آئیے چند مثالوں سے احتمال کو سیکھتے ہیں:
1) اگر 52 کارڈز کے اچھی طرح سے بدلے ہوئے ڈیک سے ایک کارڈ تیار کیا گیا ہے، تو ملکہ کے ڈرائنگ کا کیا امکان ہے؟
حل: ممکنہ نتائج کی کل تعداد = 52
52 کارڈز کے ڈیک میں 4 ملکہیں ہیں اور کوئی بھی ملکہ کھینچی جا سکتی ہے۔
لہذا، سازگار نتائج کی تعداد = 4
ملکہ بنانے کا امکان ہے \(\frac{4}{52} = \frac{1}{13}\)
2) جب نرد پھینکا جائے تو یکساں نمبر حاصل کرنے کا کیا امکان ہے؟
حل: نتائج کی کل تعداد = 6
سازگار نتائج کی کُل تعداد = 3 (یعنی نمبر 2، 4 اور 6 ہیں)
لہذا، ایک یکساں نمبر حاصل کرنے کا امکان ہے \(\frac{3}{6} = \frac{1}{2}\)